Trong Hình 12, cho tứ giác ABCD Chứng minh rằng tamg aisc ABD đồng dạng
Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của ^ADC và ^DAB=^DBC. Chứng minh rằng:
∆ABD ᔕ ∆BDC.
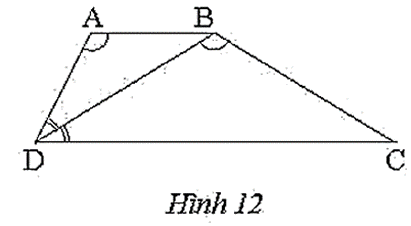
Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của ^ADC và ^DAB=^DBC. Chứng minh rằng:
∆ABD ᔕ ∆BDC.

Xét ∆ABD và ∆BDC có
^DAB=^DBC và ^ADB=^BDC (DB là tia phân giác của ^ADC).
Do đó ∆ABD ᔕ ∆BDC (g.g).