Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; góc ABI = 60 độ, góc CDx
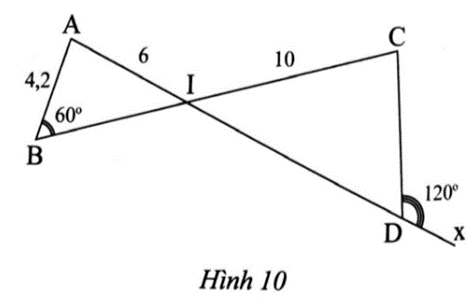
Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; \[\widehat {ABI}\] = 60°; \[\widehat {CDx}\] = 120°. Tính độ dài CD.
Ta có \[\widehat {CDx} + \widehat {CDI} = 180^\circ \] (hai góc kề bù).
Suy ra \[\widehat {CDI} = 180^\circ - \widehat {CDI} = 180^\circ - 120^\circ = 60^\circ \].
Xét ∆IAB và ∆ICD có
\[\widehat {ABI} = \widehat {CDI}\] (= 60°) và \[\widehat {AIB} = \widehat {CID}\] (đối đỉnh).
Suy ra ∆IAB ᔕ ∆ICD (g.g).
Suy ra \[\frac{{IA}}{{IC}} = \frac{{AB}}{{CD}}\] hay \[\frac{6}{{10}} = \frac{{4,2}}{{CD}}\].
Do đó \[CD = \frac{{4,2.10}}{6} = 7\].
Vậy CD = 7.