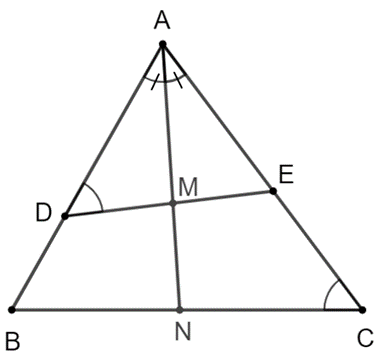
Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho \[\widehat {ADE} = \widehat {ACB}\].
Tia phân giác của \[\widehat {BAC}\] cắt DE tại M và cắt BC tại N.
Chứng minh rằng ME . NC = MD . NB.
Ta có ∆AED ᔕ ∆ABC suy ra \[\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\] hay \[\frac{{AE}}{{AD}} = \frac{{AB}}{{AC}}\] (1)
• Vì AM là tia phân giác của \[\widehat {DAE}\] nên \[\frac{{ME}}{{MD}} = \frac{{AE}}{{AD}}\] (2)
• Vì AN là tia phân giác của \[\widehat {BAC}\] nên \[\frac{{NB}}{{NC}} = \frac{{AB}}{{AC}}\] (3)
Từ (1); (2) và (3) suy ra \[\frac{{ME}}{{MD}} = \frac{{NB}}{{NC}}\] hay ME . NC = MD . NB (đpcm).