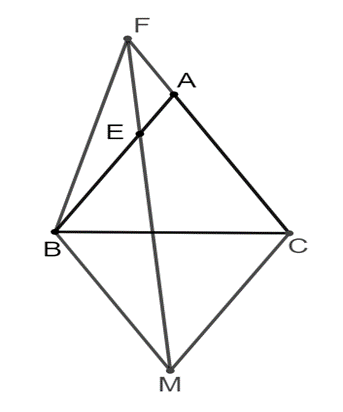
Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB tại E và cắt AC tại F. Chứng minh rằng:
\[\frac{{CA}}{{CF}} = \frac{{ME}}{{MF}}\] và \[\frac{{BE}}{{BA}} = \frac{{ME}}{{MF}}\].
Xét ∆MCF có AE // CM (vì AB // CM), theo định lí Thalès ta có:
\[\frac{{CA}}{{CF}} = \frac{{ME}}{{MF}}\] (1)
Xét ∆BEM có AF // BM (vì AC // BM), theo hệ quả của định lí Thalès ta có:
\[\frac{{AE}}{{BE}} = \frac{{EF}}{{ME}}\].
Ta có \[\frac{{AE}}{{BE}} + 1 = \frac{{EF}}{{ME}} + 1\] hay \[\frac{{AE}}{{BE}} + \frac{{BE}}{{BE}} = \frac{{EF}}{{ME}} + \frac{{ME}}{{ME}}\].
Suy ra \[\frac{{BA}}{{BE}} = \frac{{MF}}{{ME}}\] hay \[\frac{{BE}}{{BA}} = \frac{{ME}}{{MF}}\] (2)