Đáp án A

Phương pháp:

Giải phương trình và biểu diễn trên đường tròn đơn vị.

Cách giải:

Ta có:

\(cos2x - \sin x \Leftrightarrow cos2x = \sin x \Leftrightarrow cos2x = cos\left( {\frac{\pi }{2} - x} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{2} - x + k2\pi \\2x = - \frac{\pi }{2} + x + k2\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{\pi }{6} + \frac{{k2\pi }}{3}\\x = - \frac{\pi }{2} + k2\pi \end{array} \right.,\,k \in \mathbb{Z}\)

Biểu diễn trên đường tròn đơn vị:

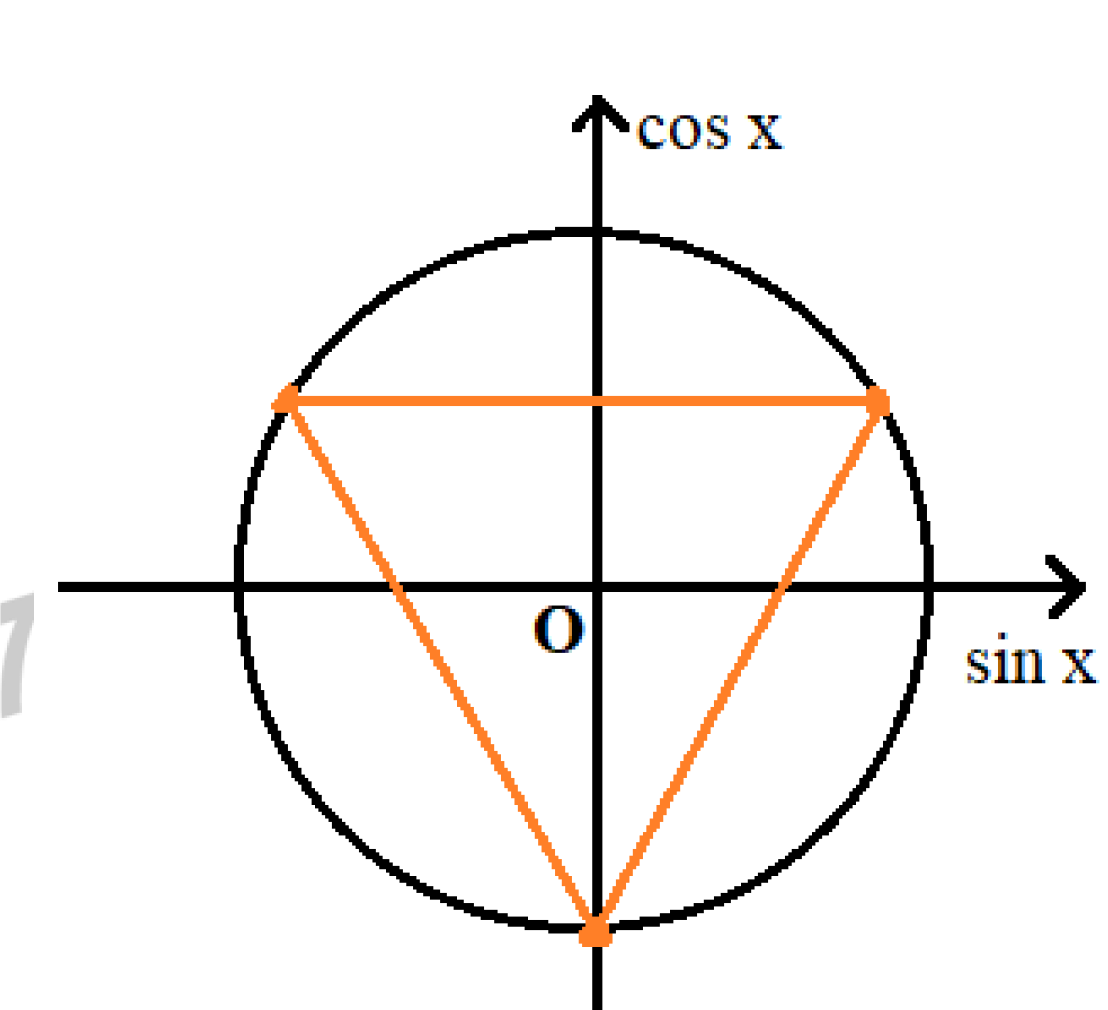
Từ hình vẽ ta thấy có tất cả 3 điểm biểu diễn nghiệm của phương trình trên đường tròn đơn vị.