Quan sát Hình 44, biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC. Vì sao hai đường thẳng MF và AB song song với nhau

Bài 34 trang 115 SBT Toán 7 Tập 1:

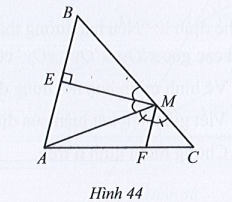
Quan sát Hình 44, biết ME vuông góc với AB tại E và ME, MF lần lượt là tia phân giác của góc AMB và AMC. Vì sao hai đường thẳng MF và AB song song với nhau?

Trả lời

Vì ME, MF lần lượt là tia phân giác của góc AMB và AMC nên:

$\widehat{AME}=\widehat{BME}=\frac{1}{2}\widehat{AMB}$ và $\widehat{AMF}=\widehat{CMF}=\frac{1}{2}\widehat{AMC}$

Mặt khác $\widehat{AMB}$ và $\widehat{AMC}$ là hai góc kề bù nên ta có:

$\widehat{AMB}+\widehat{AMC}=180°$

Lại có $\widehat{AME}$ và $\widehat{AMF}$ là hai góc kề nhau nên:

$\widehat{AME}+\widehat{AMF}=\widehat{EMF}$

Do đó 

$$\begin{gathered} \widehat{EMF}=\widehat{AME}+\widehat{AMF} \\ =\frac{1}{2}\widehat{AMB}+\frac{1}{2}\widehat{AMC} \end{gathered}$$

Hay

$$\begin{gathered} \widehat{EMF}=\frac{1}{2}\left(\widehat{AMB}+\widehat{AMC}\right) \\ =\frac{1}{2}.180°=90°. \end{gathered}$$

Suy ra $\widehat{EMF}=\widehat{BEM}$ (cùng bằng 90°).

Mà $\widehat{EMF}$ và $\widehat{BEM}$ là hai góc so le trong nên MF // AB.

Vậy MF và AB song song với nhau.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 3: Hai đường thẳng song song

Bài 4: Định lí

Bài tập cuối chương 4

Bài 1: Thu thập, phân loại và biểu diễn dữ liệu

Bài 2: Phân tích và xử lí số liệu

Bài 3: Biểu đồ đoạn thẳng