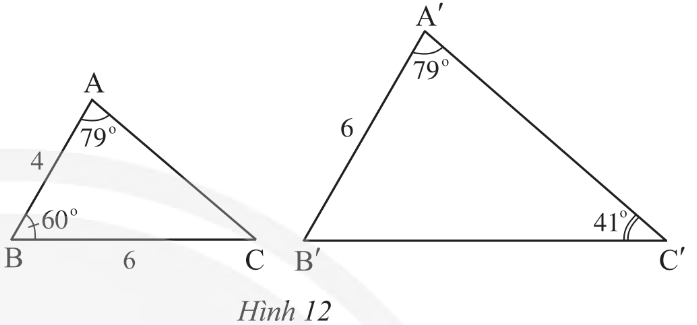
Quan sát Hình 12.

a) Chứng minh rằng ΔABC ᔕ ΔA′B′C′.

b) Tính độ dài B'C'.

Lời giải:

a) Tam giác ABC có: \[\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 41^\circ \].

Xét ΔABC và ΔA'B'C' có:

\[\widehat A = \widehat {A'} = 79^\circ \]

\[\widehat C = \widehat {C'} = 41^\circ \]

Suy ra ΔABC ᔕ ΔA′B′C′ (g.g).

b) ΔABC ᔕ ΔA′B′C′ nên \[\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\] (các cạnh tương ứng tỉ lệ

Hay \[\frac{4}{6} = \frac{6}{{B'C'}}\] nên \[B'C' = \frac{{6\,.\,6}}{4} = 9\] (cm).

Vậy B'C' = 9 cm.