a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm
12
31/10/2024
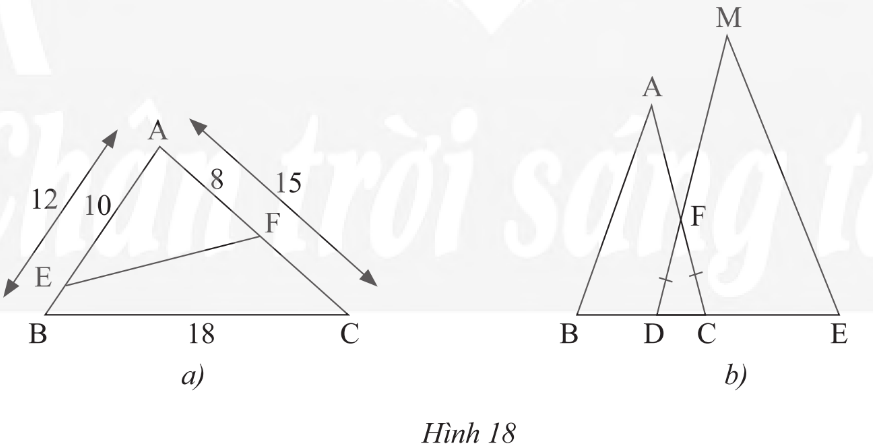
a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm (Hình 18a). Tính độ dài đoạn thẳng EF.
b) Trong Hình 18b, cho biết FD = FC, BC = 9 dm, DE = 12 dm, AC = 15 dm, MD = 20 dm. Chứng minh rằng ΔABC ᔕ ΔMED.
Trả lời
Lời giải:
a) Xét ΔAFE và ΔABC có:
\[\frac{{AF}}{{AB}} = \frac{{AE}}{{AC}} = \frac{2}{3}\]
\[\widehat A\] chung
Do đó ΔAFE ᔕ ΔABC (c.g.c)
Suy ra \[\frac{{AF}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{EF}}{{BC}}\] (các cặp cạnh tương ứng).
Khi đó \[\frac{8}{{12}} = \frac{{10}}{{15}} = \frac{{EF}}{{18}} = \frac{2}{3}\] suy ra \[EF = \frac{{18\,.\,2}}{3} = 12\] (cm).
Vậy EF = 12 cm.
b) Xét ΔABC và ΔMED ta có:
\[\frac{{BC}}{{ED}} = \frac{{AC}}{{MD}} = \frac{3}{4}\]
\[\widehat C = \widehat D\] (tam giác FDC cân)
Vậy ΔABC ᔕ ΔMED (c.g.c).
Trường hợp đồng dạng thứ ba (g.g)

