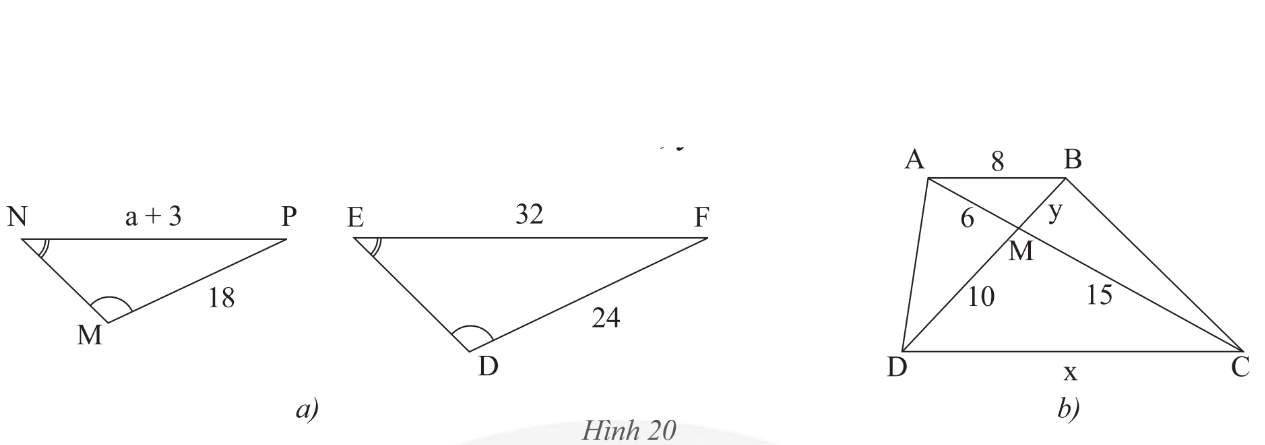
a) Trong Hình 20a, cho biết \[\widehat N = \widehat E,\;\widehat M = \widehat D\], MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a.

b) Cho ABCD là hình thang (AB // CD) (Hình 20b).

Chứng minh rằng ΔAMB ᔕ ΔCMD. Tìm x, y.

Lời giải:

a) Xét ΔMNP và ΔDEF có:

\[\widehat N = \widehat E,\;\widehat M = \widehat D\]

Do đó ΔMNP ᔕ ΔDEF (g.g)

Suy ra \[\frac{{NP}}{{EF}} = \frac{{MP}}{{DF}}\] (các cạnh tương ứng).

Khi đó \[\frac{{a + 3}}{{32}} = \frac{{18}}{{24}} = \frac{3}{4}\] nên \[a + 3 = \frac{{32\,.\,\,3}}{4} = 24\] (cm).

Vậy a = 24 – 3 = 21.

b) Xét hình thang ABCD (AB // CD):

Vì AB // CD nên \[\widehat {MAB} = \widehat {MCD},\;\widehat {MBA} = \widehat {MDC}\;\] (cặp góc so le trong).

Xét ΔAMB và ΔCMD có:

\[\widehat {MAB} = \widehat {MCD}\;\] (chứng minh trên)

\[\widehat {MBA} = \widehat {MDC}\] (chứng minh trên)

Do đó ΔAMB ᔕ ΔCMD (g.g)

Suy ra \[\frac{{AM}}{{CM}} = \frac{{MB}}{{MD}} = \frac{{AB}}{{CD}}\] (các cặp cạnh tương ứng).

Khi đó \[\frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\].

Suy ra \[x = \frac{{15\,.\,8}}{6} = 20;y = \frac{{6\,.\,10}}{{15}} = 4\].

Vậy x = 20; y = 4.