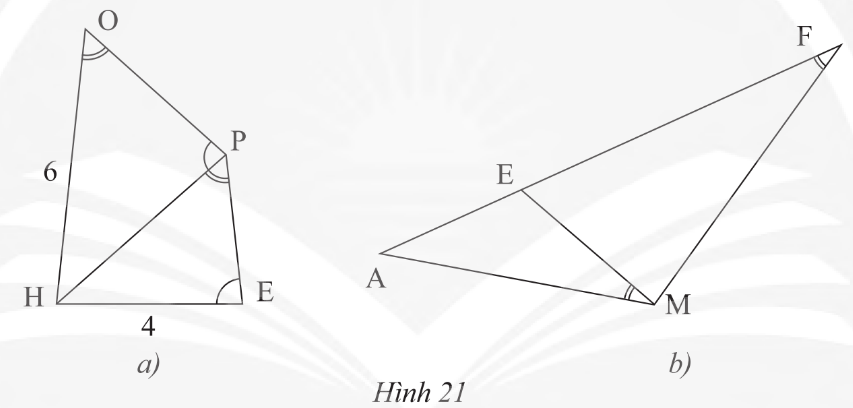
a) Trong Hình 21a, cho biết \[\widehat {HOP} = \widehat {HPE},\;\widehat {HPO} = \widehat {HEP}\], OH = 6 cm và HE = 4 cm. Tính độ dài đoạn thẳng HP.

b) Trong Hình 21b, cho biết \[\widehat {AME} = \widehat {AFM}\]. Chứng minh rằng AM² = AE.AF.

Lời giải:

a) Xét ΔHOP và ΔHPE có: 

\[\widehat {HOP} = \widehat {HPE}\] (gt)

\[\widehat {HPO} = \widehat {HEP}\] (gt)

Do đó ΔHOP ᔕ ΔHPE (g.g)

Suy ra \[\frac{{HO}}{{HP}} = \frac{{HP}}{{HE}}\] (các cặp cạnh tương ứng).

Khi đó \[\frac{6}{{HP}} = \frac{{HP}}{4}\] nên HP = 6.4 = 24.

Vậy \[HP = 2\sqrt 6 \] cm.

b) Xét ΔAEM và ΔAMF ta có:

\[\widehat A\] chung

\[\widehat {AME} = \widehat {AFM}\]

Do đó ΔAEM ᔕ ΔAMF (g.g)

Suy ra \[\frac{{AE}}{{AM}} = \frac{{AM}}{{AF}}\] nên AM² = AE.AF (đpcm).