Quan sát đồ thị hàm số y = cosx ở Hình 27. a) Nêu tập giá trị của hàm số y = cosx.
273
16/05/2023
Hoạt động 8 trang 27 Toán 11 Tập 1: Quan sát đồ thị hàm số y = cosx ở Hình 27.
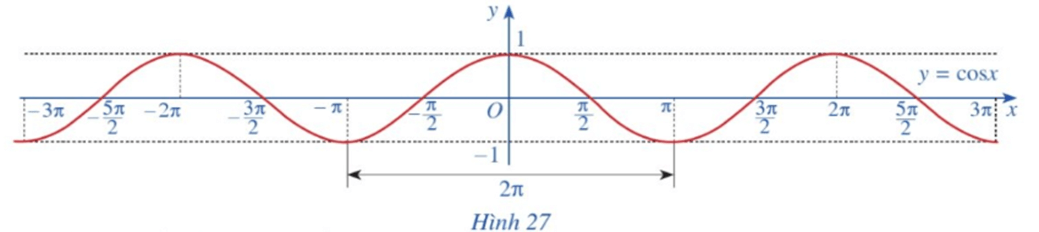
a) Nêu tập giá trị của hàm số y = cosx.
b) Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cosx.
c) Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π] hay không? Hàm số y = cosx có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số y = cosx.
Trả lời
a) Tập giá trị của hàm số y = cosx là [‒1; 1].
b) Trục tung là trục đối xứng của đồ thị hàm số.
Do đó hàm số y = cosx là hàm số chẵn.
c)
‒ Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta sẽ nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π].
Làm tương tự như trên ta sẽ được đồ thị hàm số y = cosx trên ℝ.
‒ Xét hàm số f(x) = y = cosx trên ℝ, với T = 2π và x ∈ ℝ ta có:
• x + 2π ∈ ℝ và x – 2π ∈ ℝ;
• f(x + 2π) = f(x)
Do đó hàm số y = cosx là hàm số tuần hoàn với chu kì T = 2π.
d) Quan sát đồ thị hàm số y = cosx ta thấy:
• Hàm số đồng biến trên mỗi khoảng (‒3π; ‒2π); (‒π; 0); (π; 2π); …
Ta có: (‒3π; ‒2π) = (‒π ‒ 2π; 0 ‒ 2π);
(π; 2π) = (‒π + 2π; 0 + 2π);
…
Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng (‒π + k2π; k2π) với k ∈ ℤ.
• Hàm số nghịch biến trên mỗi khoảng (‒2π; ‒π); (0; π); (2π; 3π); …
Ta có: (‒2π; ‒π) = (0 ‒ 2π; π ‒ 2π);
(2π; 3π) = (0 + 2π; π + 2π);
…
Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng (k2π; π + k2π) với k ∈ ℤ.
Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Bài 2: Các phép biến đổi lượng giác
Bài 3: Hàm số lượng giác và đồ thị
Bài 4: Phương trình lượng giác cơ bản
Bài tập cuối chương 1
Bài 1: Dãy số

