Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ)

Bài 6 trang 31 Toán 11 Tập 1: Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ), trong đó t là thời gian tính bằng giây, A là biên độ dao động và x là li độ dao động đều được tính bằng centimét. Khi đó, chu kì T của dao động là T=$\frac{2\pi }{\omega }$. Xác định giá trị của li độ khi t = 0, $t=\frac{T}{4},t=\frac{T}{2},t=\frac{3T}{4}$, t = T và vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong trường hợp:

a) A = 3 cm, φ = 0;

b) A = 3 cm, $\phi =-\frac{\pi }{2}$;

c) A = 3 cm, $\phi =\frac{\pi }{2}$.

Trả lời

Từ T = $\frac{2\pi }{\omega }$ ta có $\omega =\frac{2\pi }{T}$.

Khi đó ta có phương trình li độ là x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$.

a)

‒ Với A = 3 cm và φ = 0 thay vào phương trình li độ x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$ ta có:

x = 3cos$\left(\frac{2\pi }{T}.t\right)$.

• t = 0 thì x = 3cos0 = 3;

• t = $\frac{T}{4}$ thì x = 3cos$\left(\frac{2\pi }{T}.\frac{T}{4}\right)$= 3cos$\frac{\pi }{2}$ = 0;

• t = $\frac{T}{2}$ thì x = 3cos$\left(\frac{2\pi }{T}.\frac{T}{2}\right)$ = 3cos$\pi$ = -3

• t = $\frac{3T}{4}$ thì x = 3cos$\left(\frac{2\pi }{T}.\frac{3T}{4}\right)$ = 3cos$\frac{3\pi }{2}$ = 0;

• t = T thì x = 3cos$\left(\frac{2\pi }{T}.T\right)$ = 3cos2$\pi$ = 3

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T]:

Xét hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ có chu kì là T.

Ta vẽ đồ thị hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] theo bảng sau:

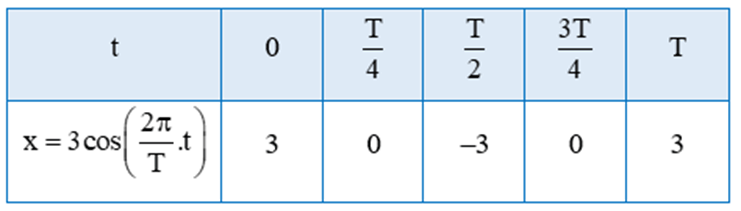
Bằng cách dịch chuyển đồ thị hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [T; 2T].

Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà x = 3cos$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T] như sau:

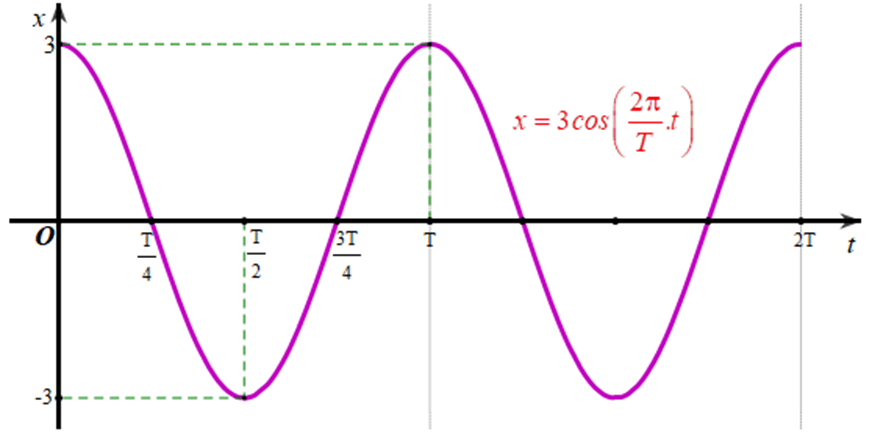
b)

‒ Với A = 3 cm và $\phi =-\frac{\pi }{2}$ thay vào phương trình li độ x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$ ta có:

x = 3cos$\left(\frac{2\pi }{T}.t-\frac{\pi }{2}\right)$ = 3cos$\left(\frac{\pi }{2}-\frac{2\pi }{T}.t\right)$ = 3sin$\left(\frac{2\pi }{T}.t\right)$

• t = 0 thì x = 3sin$\left(\frac{2\pi }{T}.0\right)$ = 3sin0 = 0

• t = $\frac{T}{4}$ thì x = 3sin$\left(\frac{2\pi }{T}.\frac{T}{4}\right)$ = 3sin$\frac{\pi }{2}$ = 3;

• t = $\frac{T}{2}$ thì x = 3sin$\left(\frac{2\pi }{T}.\frac{T}{2}\right)$ = 3sin$\pi$ = 0;

• t = $\frac{3T}{4}$ thì x = 3sin$\left(\frac{2\pi }{T}.\frac{3T}{4}\right)$ = 3sin$\frac{3\pi }{2}$ = -3;

• t = T thì x = 3sin$\left(\frac{2\pi }{T}.T\right)$ = 3sin2$\pi$ = 0.

‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T]:

Xét hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ có chu kì là T.

Ta vẽ đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] theo bảng sau:

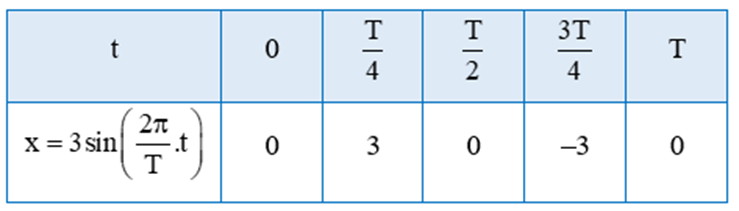
Bằng cách dịch chuyển đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [T; 2T].

Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà x = 3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T] như sau:

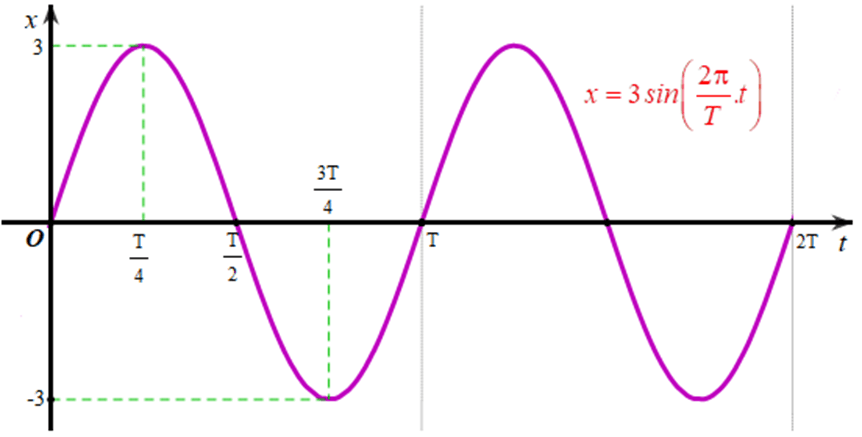
c)

‒ Với A = 3 cm và $\phi =\frac{\pi }{2}$ thay vào phương trình li độ x = Acos$\left(\frac{2\pi }{T}.t+\phi \right)$ ta có:

x = 3cos$\left(\frac{2\pi }{T}.t+\frac{\pi }{2}\right)$ = -3cos$\left(\pi -\left(\frac{2\pi }{T}.t+\frac{\pi }{2}\right)\right)$

= -3cos$\left(\frac{\pi }{2}-\frac{2\pi }{T}.t\right)$ = -3sin$\left(\frac{2\pi }{T}.t\right)$

• t = 0 thì x = -3sin$\left(\frac{2\pi }{T}.0\right)$ = -3sin0 = 0

• t = $\frac{T}{4}$ thì x = -3sin$\left(\frac{2\pi }{T}.\frac{T}{4}\right)$ = -3sin$\frac{\pi }{2}$ = -3;

• t = $\frac{T}{2}$ thì x = -3sin$\left(\frac{2\pi }{T}.\frac{T}{2}\right)$ = -3sin$\pi$ = 0;

• t = $\frac{3T}{4}$ thì x = -3sin$\left(\frac{2\pi }{T}.\frac{3T}{4}\right)$ = -3sin$\frac{3\pi }{2}$ = 3;

• t = T thì x = -3sin$\left(\frac{2\pi }{T}.T\right)$ = -3sin2$\pi$ = 0.

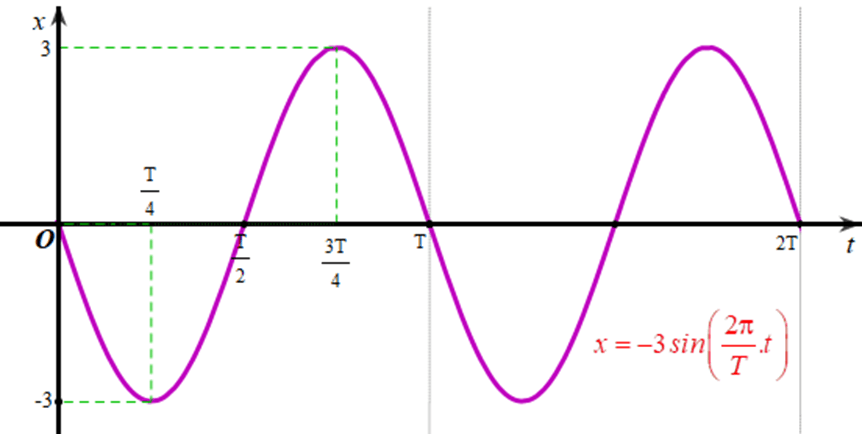
‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà x = -3sin$\left(\frac{2\pi }{T}.t\right)$ trên đoạn [0; 2T]:

Đồ thị hàm số x = -3sin$\left(\frac{2\pi }{T}.t\right)$ là hình đối xứng với đồ thị hàm số x = 3sin$\left(\frac{2\pi }{T}.t\right)$ qua trục hoành:

Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

Bài 2: Các phép biến đổi lượng giác

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 1: Dãy số