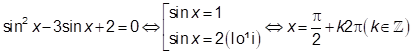Nghiệm của phương trình sin ^2x - 3sin x + 2 = 0 là: A. x = pi + k2pi ,k thuộc Z B. x = - pi /2 + k2pi ,k thuộc Z C. x = pi /2 + k2pi ,k thuộc Z D. x = k2pi ,k thuộc Z
Nghiệm của phương trình \[{\sin ^2}x - 3\sin x + 2 = 0\] là:
A. \[x = \pi + k2\pi ,k \in \mathbb{Z}.\]
B. \[x = - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\]
C. \[x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\]
D. \[x = k2\pi ,k \in \mathbb{Z}.\]