Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang. Công suất P
Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang. Công suất P được xác định bởi tích của lực kéo về và vận tốc của vật là đại lượng đặc trưng cho tốc độ chuyển hóa giữa thế năng và động năng. Hình bên là đồ thị biểu diễn sự phụ thuộc của P theo thời gian t. Tại thòi điểm ban đầu t=0, vật cách vị trí cân bằng 5cm. Độ cứng của lò xo là
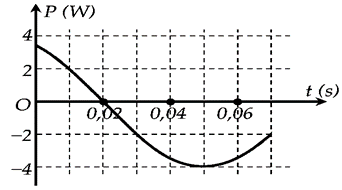
A. 30,6N/m
B. 22,1N/m
C. 11,5N/m
D. 15,3N/m
