Mặt bên của một chiếc va li (Hình 17a) có dạng hình thang cân và được vẽ lại

Bài 7 trang 72 Toán 8 Tập 1: Mặt bên của một chiếc va li (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là 60 cm, cạnh bên là 61 cm và đáy lớn là 92 cm. Tính độ dài đáy nhỏ.

Trả lời

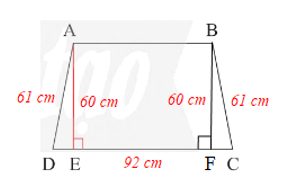
Áp dụng định lí Pythagore vào DADE vuông tại E, ta có:

AD² = AE² + DE²

Suy ra DE² = AD² – AE² = 61² – 60² = 3 721 – 3 600 = 121 = 11²

Do đó DE = 11 cm.

Kẻ BF ⊥ CD, khi đó BF là đường cao của hình thang cân ABCD nên BF = 60 cm.

Xét DADE và DBCF có:

$$$\widehat{AED}=\widehat{BFC}=90°$;

AD = BC (do ABCD là hình thang cân);

$\widehat{ADE}=\widehat{BCF}$ (do ABCD là hình thang cân).

Do đó DADE = DBCF (cạnh huyền – góc nhọn)

Suy ra DE = CF = 11 cm (hai cạnh tương ứng).

Mà DE + EF + CF = DC

Nên EF = DC – DE – CF = 92 – 11 – 11 = 70 cm.

Tương tự Vận dụng 4, trang 71, Sách giáo khoa Toán 8, tập một, ta dễ dàng chứng minh được AB = EF = 70 cm.

Vậy độ dài đáy nhỏ của hình thang cân là 70 cm.

Xem thêm lời giải bài tập SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi

Bài 5: Hình chữ nhật – Hình vuông

Bài tập cuối chương 3