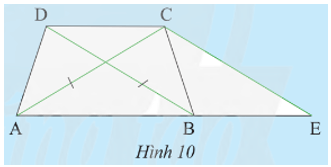
Cho hình thang ABCD có hai đáy là AB, CD và có hai đường chéo bằng nhau

Khám phá 3 trang 70 Toán 8 Tập 1: Cho hình thang ABCD có hai đáy là AB, CD và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua C, song song với BD và cắt AB tại E.

a) Tam giác CAE là tam giác gì? Vì sao?

b) So sánh tam giác ABD và tam giác BAC.

Trả lời

a) Xét hình thang ABCD có AB // CD hay AE // DC nên $\widehat{DCB}=\widehat{EBC}$ (so le trong)

Do DB // CE nên $\widehat{DBC}=\widehat{ECB}$ (so le trong).

Xét DDCB và DEBC có:

$\widehat{DCB}=\widehat{EBC}$ (chứng minh trên);

CB là cạnh chung;

$\widehat{DBC}=\widehat{ECB}$ (chứng minh trên).

Do đó DDCB = DEBC (g.c.g).

Suy ra BD = CE (hai cạnh tương ứng)

Mà AC = BD (giả thiết)

Nên AC = CE.

Xét DACE có AC = CE nên là tam giác cân tại C.

b) Do DACE cân tại C (câu a) nên $\widehat{CAE}=\widehat{CEA}$ (hai góc tương ứng).

Mặt khác DB // CE nên $\widehat{DBA}=\widehat{CEA}$ (đồng vị).

Do đó $\widehat{CAE}=\widehat{DBA}\left(=\widehat{CEA}\right)$.

Xét DABD và DBAC có:

AB là cạnh chung;

$\widehat{DBA}=\widehat{CAB}$ (chứng minh trên);

BD = AC (giả thiết).

Do đó DABD = DBAC (c.g.c).

Xem thêm lời giải bài tập SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi

Bài 5: Hình chữ nhật – Hình vuông

Bài tập cuối chương 3