Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao

Bài 31 trang 77 SBT Toán 7 Tập 2: Hai đoạn thẳng BE và CD vuông góc với nhau tại A sao cho AB = AD, AC = AE, AB > AC. Trong các phát biểu sau, phát biểu nào sai? Vì sao?

a) ΔAED = ΔACB. b) DE = BC.

c) ΔACE = ΔABD. d) $\widehat{ABC}=\widehat{A\text{ED}}$.

Trả lời

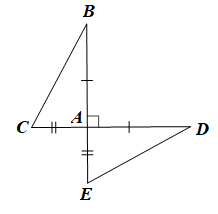
Xét ΔAED và ΔACB có:

$\widehat{DA\text{E}}=\widehat{BAC}$ (cùng bằng 90°),

AD = AB (giả thiết),

AE = AC (giả thiết)

Do đó ΔAED = ΔACB (hai cạnh góc vuông) nên phát biểu a đúng.

Từ ΔAED = ΔACB, suy ra:

• DE = BC (hai cạnh tương ứng), nên phát biểu b đúng.

• $\widehat{ABC}=\widehat{A\text{DE}}$(hai góc tương ứng) nên phát biểu d sai.

Xét $∆$ACE và $∆$ABD, ta thấy hai tam giác này không có các cạnh bằng nhau, các góc bằng nhau. Do đó hai tam giác này không bằng nhau, nên phát biểu c sai.

Vậy phát biểu c, d là phát biểu sai.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 3. Hai tam giác bằng nhau

Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6. Trường hợp bằng nhau thứ ba của tam giác:

Bài 7. Tam giác cân

Bài 8. Đường vuông góc và đường xiên