Bài 35 trang 78 SBT Toán 7 Tập 2: Cho tam giác ABC có , AH vuông góc với BC (H thuộc BC). Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho BD = HA (Hình 23).
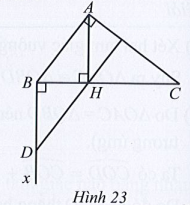
a) Chứng minh ∆AHB = ∆DBH.
b) Chứng minh DH vuông góc với AC.
c) Tính số đo góc BDH.
a) Xét ∆AHB và ∆DBH có:
(cùng bằng 90°),
BH là cạnh chung,
AH = BD (giả thiết),
Suy ra ∆AHB = ∆DBH (hai cạnh góc vuông).
Vậy ∆AHB = ∆DBH.
b) Do ∆AHB = ∆DBH (chứng minh câu a) nên (hai góc tương ứng).
Mà ở vị trí so le trong
Do đó AB // DH.
Lại có, AB ⊥ AC nên DH ⊥ AC (một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại).
Vậy DH ⊥ AC.
c) Do ∆AHB = ∆DBH (chứng minh câu a) nên (hai góc tương ứng).
Xét tam giác ABH vuông tại H có:
(trong tam giác vuông, tổng hai góc nhọn bằng 90°).
Suy ra .
Do đó .
Vậy .
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh
Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh