Đáp án A

Phương pháp:

Xét trên đường tròn lượng giác.

Cách giải:

Ta có\[x \in \left[ { - \frac{\pi }{3};\frac{\pi }{6}} \right] \Rightarrow 2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right].\]

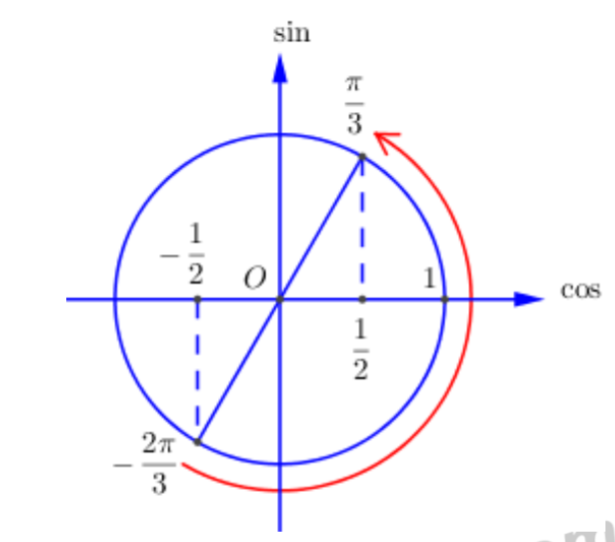
Biểu diễn trên đường tròn lượng giác:

Dựa vào đường tròn lượng giác ta thấy với\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};1} \right].\]

Vậy\[M = 1;m = - \frac{1}{2} \Rightarrow T = M - 2m = 1 - 2.\left( { - \frac{1}{2}} \right) = 2.\]

Chú ý: Cần biểu diễn trên đường tròn lượng giác, nhiều học sinh nhầm lẫn\[2x \in \left[ { - \frac{{2\pi }}{3};\frac{\pi }{3}} \right] \Rightarrow \cos 2x \in \left[ { - \frac{1}{2};\frac{1}{2}} \right].\]