Đáp án D
Phương pháp:
Sử dụng phép quay tâm I góc quay \[\alpha \] biến M thành M’ thì \[OM = OM'\] và \[\angle \left( {OM;\,\,OM'} \right) = \alpha \]
Cách giải:
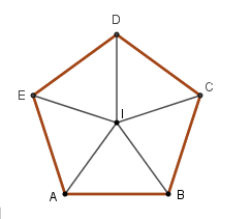
Vì ABCDE là ngũ giác đều tâm I nên \[IA = IB = IC = ID = IE\] và \[\widehat {CID} = \widehat {DIE} = \widehat {EIA} = \widehat {AIB} = \widehat {BIC} = \frac{{360^\circ }}{5} = 72^\circ \]
Từ đó ta có
\[{Q_{\left( {I;144^\circ } \right)}}\left( C \right) = E;\,\,{Q_{\left( {I;\,\,144^\circ } \right)}}\left( D \right) = A \Rightarrow {Q_{\left( {I;\,\,144^\circ } \right)}}\left( {CD} \right) = EA\] nên A đúng
\[{Q_{\left( {I;\,\,72^\circ } \right)}}\left( A \right) = B;\,\,{Q_{\left( {I;\,\,72^\circ } \right)}}\left( B \right) = C \Rightarrow {Q_{\left( {I;\,\,72^\circ } \right)}}\left( {AB} \right) = BC\] nên B đúng
\[{Q_{\left( {I;\,\,72^\circ } \right)}}\left( A \right) = B;\,\,{Q_{\left( {I;\,\,72^\circ } \right)}}\left( E \right) = A \Rightarrow {Q_{\left( {I;\,\,72^\circ } \right)}}\left( {AE} \right) = BA\] nên C đúng
\[{Q_{\left( {I;\,\,144^\circ } \right)}}\left( B \right) = D;\,\,{Q_{\left( {I;\,\,144^\circ } \right)}}\left( C \right) = E \Rightarrow {Q_{\left( {I;\,\,144^\circ } \right)}}\left( {BC} \right) = DE\] nên D sai.
