Gọi E là trung điểm của BC và I là giao điểm của AE với MN. Chứng minh I là
Cho tam giác nhọn ABC có M, N lần lượt là trung điểm của AB, AC.
Gọi E là trung điểm của BC và I là giao điểm của AE với MN. Chứng minh I là trung điểm của MN.
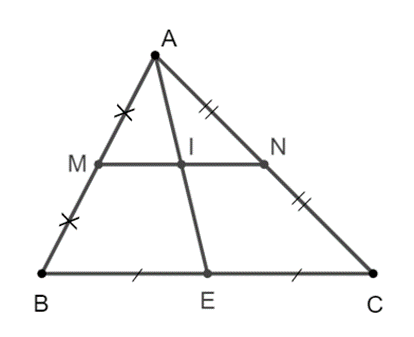
Xét ∆ABE, ta có MA = MB và MI // BE (vì I ∈ MN, E ∈ BC) nên IA = IE.
Do đó MI là đường trung bình của ∆ABE, suy ra MI = \[\frac{{BE}}{2}\].
Tương tự, ta có IN = \[\frac{{EC}}{2}\].
Mặt khác BE = EC, suy ra MI = IN.
Vậy I là trung điểm của MN.