Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // QO (M ∈ OP), IN // PO (N ∈ QO). Chứng minh:

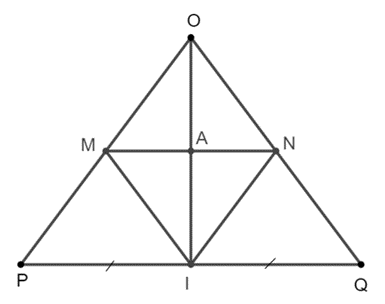
Gọi A là giao điểm của IO và MN.

∆OPQ cân tại O có OI là đường trung tuyến, suy ra OI cũng là đường cao của ∆OPQ.

Suy ra OI ⊥ PQ     (1)

Xét ∆OPQ, ta có MO = MP và NO = NQ nên MN là đường trung bình của ∆OPQ.

Suy ra MN // PQ   (2)

Từ (1) và (2) suy ra MN ⊥ OI tại A hay MN ⊥ IA.

Mà ∆IMN cân tại I có IA là đường cao nên IA cũng là đường trung trực của MN.

Do đó, OI là đường trung trực của MN.