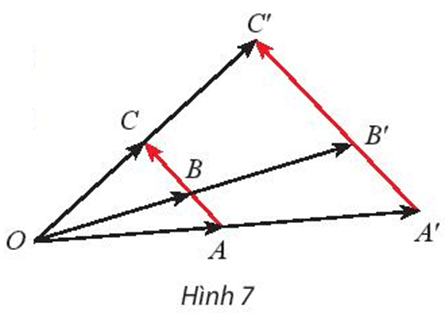
Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự V(O, k). Cho biết 

Khám phá 3 trang 33 Chuyên đề Toán 11: Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự V_{(O, k)}. Cho biết $\overrightarrow{\mathrm{BA}}=m\overrightarrow{\mathrm{BC}}$, hai vectơ $\overrightarrow{B^{\text{'}}{A}^{\text{'}}}$ và $m\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$ có bằng nhau không?

Trả lời

Theo bài, ta có A’, B’ lần lượt là ảnh của A, B qua V_{(O, k)}.

Áp dụng tính chất 1, ta được $\overrightarrow{B^{\text{'}}{A}^{\text{'}}}=k\overrightarrow{\mathrm{BA}}$.

Chứng minh tương tự, ta được $\overrightarrow{B^{\text{'}}{C}^{\text{'}}}=k\overrightarrow{\mathrm{BC}}$.

Ta có $\overrightarrow{B^{\text{'}}{A}^{\text{'}}}=k\overrightarrow{\mathrm{BA}}=k.m\overrightarrow{\mathrm{BC}}=m.k\overrightarrow{\mathrm{BC}}=m\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$.

Vậy hai vectơ $\overrightarrow{B^{\text{'}}{A}^{\text{'}}}$ và $m\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$ bằng nhau.

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Phép đối xứng tâm

Bài 5: Phép quay

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1

Bài 1: Đồ thị