Cho hình thang ABCD có hai đáy là AB và CD với CD =1/2 AB . Gọi I là giao điểm của hai đường chéo AC

Bài 6 trang 36 Chuyên đề Toán 11: Cho hình thang ABCD có hai đáy là AB và CD với $\mathrm{CD}=\frac{1}{2}\mathrm{AB}$. Gọi I là giao điểm của hai đường chéo AC và BD. Tìm phép vị tự biến $\overrightarrow{\mathrm{AB}}$ thành $\overrightarrow{\mathrm{CD}}$.

Trả lời

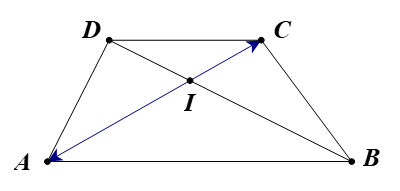
Vì ABCD là hình thang nên AB // CD

Ta có I là giao điểm của hai đường chéo AC và BD, áp dụng hệ quả định lí Thales, ta được $\frac{\mathrm{IC}}{\mathrm{IA}}=\frac{\mathrm{IB}}{\mathrm{ID}}=\frac{\mathrm{CD}}{\mathrm{AB}}=\frac{1}{2}$.

Suy ra $\mathrm{IC}=\frac{1}{2}\mathrm{IA}$.

Mà A, C nằm khác phía so với I.

Do đó $\overrightarrow{\mathrm{IC}}=-\frac{1}{2}\overrightarrow{\mathrm{IA}}$.

Vì vậy $V_{\left(I,-\frac{1}{2}\right)}\left(A\right)=C$.

Chứng minh tương tự, ta được $V_{\left(I,-\frac{1}{2}\right)}\left(B\right)=D$.

Khi đó qua phép vị tự $V_{\left(I,-\frac{1}{2}\right)}$ biến $\overrightarrow{\mathrm{AB}}$ thành $\overrightarrow{\mathrm{CD}}$.

Vậy phép vị tự cần tìm là $V_{\left(I,-\frac{1}{2}\right)}$.

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Phép đối xứng tâm

Bài 5: Phép quay

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1

Bài 1: Đồ thị