Góc kề bù với góc tại một đỉnh của tứ giác gọi là một góc ngoài tại đỉnh đó của tứ giác

Bài 3.6 trang 32 SBT Toán 8 Tập 1: a) Góc kề bù với góc tại một đỉnh của tứ giác gọi là một góc ngoài tại đỉnh đó của tứ giác. (Có hai góc ngoài tại một đỉnh của tứ giác, chúng đối đỉnh nên thường gọi tắt là góc ngoài tại đỉnh đó của tứ giác). Hãy tính tổng bốn góc ngoài tại bốn đỉnh của một tứ giác.

b) Định nghĩa góc ngoài tại một đỉnh của tam giác một cách tương tự. Hỏi tổng các góc ngoài của một tam giác bằng bao nhiêu?

Trả lời

a)

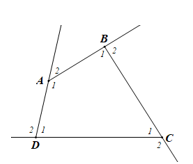
Do góc ngoài và góc tại đỉnh đó là 2 góc kề bù nên tổng bằng 180°.

Xét tứ giác ABCD (hình vẽ) có:

${\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1+{\widehat{D}}_1=360°;$

Góc ngoài tại đỉnh A là ${\widehat{A}}_2=180°-{\widehat{A}}_1;$

Góc ngoài tại đỉnh B là ${\widehat{B}}_2=180°-{\widehat{B}}_1;$

Góc ngoài tại đỉnh C là ${\widehat{C}}_2=180°-{\widehat{C}}_1;$

Góc ngoài tại đỉnh D là ${\widehat{D}}_2=180°-{\widehat{D}}_1.$

Tổng 4 góc ngoài của tứ giác ABCD là:

${\widehat{A}}_2+{\widehat{B}}_2+{\widehat{C}}_2+{\widehat{D}}_2$

$=\left(180°-{\widehat{A}}_1\right)+\left(180°-{\widehat{B}}_1\right)+\left(180°-{\widehat{C}}_1\right)+\left(180°-{\widehat{D}}_1\right)$

$=4\cdot 180°-\left({\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1+{\widehat{D}}_1\right)$

$=2\cdot 360°-360°=360°.$

b)

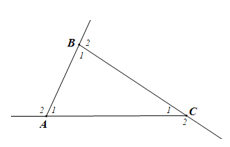
Tương tự, với tam giác ABC, ta có tổng các góc ngoài là:

${\widehat{A}}_2+{\widehat{B}}_2+{\widehat{C}}_2$

$=\left(180°-{\widehat{A}}_1\right)+\left(180°-{\widehat{B}}_1\right)+\left(180°-{\widehat{C}}_1\right)$

$=3\cdot 180°-\left({\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1\right)$

$=3\cdot 180°-180°=360°.$

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 9: Phân tích đa thức thành nhân tử

Bài tập cuối chương 2

Bài 10: Tứ giác

Bài 11: Hình thang cân

Bài 12: Hình bình hành

Bài 13: Hình chữ nhật