Gieo một đồng xu cân đối liên tiếp bốn lần. Xác suất để trong bốn lần gieo đó có ít nhất 2 lần xuất hiện mặt sấp là

A. $\frac{11}{16}$

B. $\frac{5}{16}$

C. $\frac{5}{8}$

D. $\frac{3}{8}$

Trả lời

Đáp án đúng là: A

Đồng xu cân đối nên các kết quả có thể là đồng khả năng.

Kí hiệu S và N tương ứng là đồng xu ra mặt sấp và đồng xu ra mặt ngửa.

Ta có sơ đồ hình cây mô tả không gian mẫu như sau:

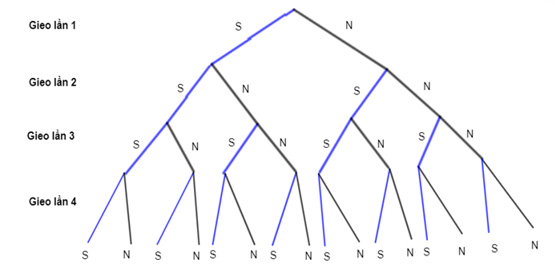
Do đó, n(Ω) = 16.

Gọi biến cố A: “Trong bốn lần gieo đó có ít nhất 2 lần xuất hiện mặt sấp”.

Theo sơ đồ hình cây ta có: 

A = {SSSS; SSSN; SSNS; SSNN; SNSS; SNSN; SNNS; NSSS; NSSN; NSNS; NNSS}.

Do đó, n(A) = 11. 

Vậy  $\text{P}\left(\text{A}\right)\text{ = }\frac{\text{n}\left(\text{A}\right)}{\text{n}\left(\text{Ω}\right)}\text{ = }\frac{11}{16}$.