Giải phương trình lượng giác sau: sin x + sin 2x/sin 3x =  - 1

Trả lời

Phương pháp:

- Sử dụng công thức cộng \[\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\] biến đổi phương trình về dạng tích.

- Giải phương trình và đối chiếu điều kiện, kết luận nghiệm.

Cách giải:

ĐK: \[\sin 3x \ne 0 \Leftrightarrow 3x \ne k\pi \Leftrightarrow x \ne \frac{{k\pi }}{3}\]

\[{\rm{PT}} \Rightarrow \sin x + \sin 2x = - \sin 3x \Leftrightarrow \left( {\sin x + \sin 3x} \right) + \sin 2x = 0\]

\[ \Leftrightarrow 2\sin 2x\cos x + \sin 2x = 0 \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\]

\[ \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\2\cos x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\\cos x = - \frac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = k\pi \\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{k\pi }}{2}\\x = \pm \frac{\pi }{3} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}\]

Biểu diễn các nghiệm trên đường tròn lượng giác ta được:

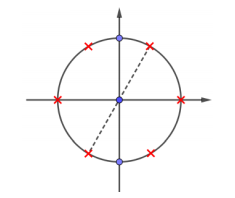
Quan sát hình vẽ ta thấy phương trình có nghiệm \[x = \frac{\pi }{2} + k\pi ,{\rm{ }}k \in \mathbb{Z}\] (hai điểm màu xanh).