Đáp án C

Phương pháp:

Tìm số nghiệm ở phương trình \(\sin x + \cos x = 1\) trong đoạn đã cho, rồi thiết lập điều kiện của m để phương trình \(\sin 4{\rm{x}} = m\) có nghiệm trong đoạn sao cho tổng hai nghiệm cả hai phương trình là bốn nghiệm phân biệt.

Cách giải:

Ta có \(\left( {\sin x + \cos x - 1} \right)\left( {\sin 4x - m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x + \cos x = 1{\rm{ }}\left( 1 \right)\\\sin 4x = m{\rm{         }}\left( 2 \right)\end{array} \right.\).

\(\left( 1 \right) \Leftrightarrow \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = 1 \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4} = \frac{\pi }{4} + k2\pi \\x + \frac{\pi }{4} = \pi - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).

+) \(\frac{\pi }{8} \le x = k2\pi \le \frac{{5\pi }}{6} \Rightarrow \frac{1}{{16}} \le k \le \frac{5}{{12}},k \in \mathbb{Z} \Rightarrow k \in \cancel{\bigcirc }\)

+) \(\frac{\pi }{8} \le x = \frac{\pi }{2} + k2\pi \le \frac{{5\pi }}{6} \Rightarrow - \frac{3}{{16}} \le k \le \frac{1}{6},k \in \mathbb{Z} \Rightarrow k = 0\)

Do đó (1) có nghiệm duy nhất là: \(x = \frac{\pi }{2}\) thỏa mãn yêu cầu.

TH1: \(x = \frac{\pi }{2}\) là 1 nghiệm của (2), khi đó ta có: \(\sin 4\frac{\pi }{2} - m = 0 \Leftrightarrow m = 0\).

Thử lại: Với \(m = 0\) thì \(\sin 4{\rm{x}} = 0 \Leftrightarrow x = \frac{{k\pi }}{4}\left( {k \in \mathbb{Z}} \right)\).

\(\frac{\pi }{8} \le \frac{{k\pi }}{4} \le \frac{{5\pi }}{6} \Leftrightarrow \frac{1}{2} \le k \le \frac{{10}}{3} \Rightarrow k \in \left\{ {1;2;3} \right\} \Rightarrow x \in \left\{ {\frac{\pi }{4};\frac{\pi }{2};\frac{{3\pi }}{4}} \right\}\).

Vậy phương trình ban đầu có 3 nghiệm phân biệt thỏa mãn yêu cầu bài toán \( \Rightarrow m = 0\) loại.

TH2: \(x = \frac{\pi }{2}\) không là nghiệm của (2) \( \Rightarrow m \ne 0\).

Khi đó để phương trình ban đầu có 4 nghiệm thỏa mãn yêu cầu bài toán thì (2) có 3 nghiệm phân biệt thỏa mãn \(x \in \left[ {\frac{\pi }{8};\frac{{5\pi }}{6}} \right]\backslash \left\{ {\frac{\pi }{2}} \right\}\).

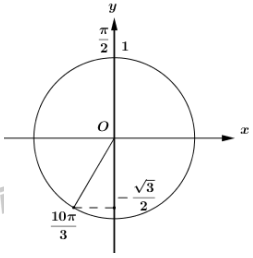
Với \(x \in \left[ {\frac{\pi }{8};\frac{{5\pi }}{6}} \right] \Rightarrow 4{\rm{x}} \in \left[ {\frac{\pi }{2};\frac{{10\pi }}{3}} \right]\), dựa vào đường tròn lượng giác ta tìm được \(m \in \left[ { - \frac{{\sqrt 3 }}{2};1} \right)\).