Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau
215
07/01/2024
Bài 4 trang 22 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
a) f(x)≥0
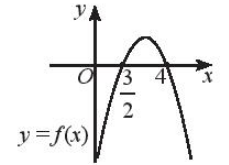
b) f(x)>0
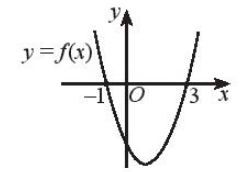
c) f(x)≤0
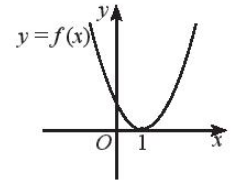
d) f(x)<0

e) f(x)<0
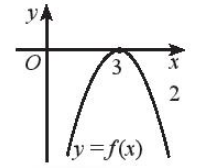
g) f(x)≤0
Trả lời
a) Ta thấy đồ thị hàm số f ( x ) cắt trục hoành tại hai điểm x = 32 và x = 4, khi 32 ≤ x ≤ 4 thì đồ thị hàm số nằm trên trục hoành nên f(x)≥0 khi 32 ≤ x ≤ 4.
Vậy f(x) ≥ 0 khi x ∈ [32;4].
b) f(x)>0 khi đồ thị hàm số f ( x ) nằm trên trục hoành hay x < –1 hoặc x > 3.
Vậy f(x) > 0 khi (– ∞; – 1) ∪ (3; +∞).
c) Dựa vào hình vẽ ta thấy:
Đồ thị hàm số cắt trục hoành tại x = 1.
Với x ≠ 1 đồ thị hàm số nằm hoàn toàn phía trên trục hoành.
Do đó f(x) ≤ 0 khi x = 1.
Vậy f(x) ≤ 0 khi x = 1.
d) f(x)<0 vô nghiệm vì ta thấy đồ thị hàm số f ( x ) hoàn toàn nằm trên trục hoành.
Vậy không tồn tại giá trị của x để f(x) < 0.
e) Dựa vào hình vẽ ta thấy:
Đồ thị hàm số cắt trục hoành tại x = 3.
Đồ thị nằm hoàn toàn phía dưới trục hoành với x ≠ 3.
Do đó f(x)<0 khi x ≠ 3.
Vậy f(x) < 0 khi x ≠ 3.
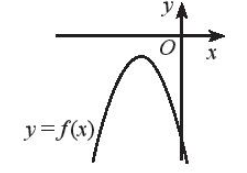
g) Ta có thể thấy đồ thị hàm số f ( x ) hoàn toàn nằm dưới trục hoành nên f(x)≤0 với mọi x ∈ ℝ.
Vậy f(x) ≤ 0 với mọi x ∈ ℝ.
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giải bất phương trình bậc hai một ẩn
Bài 3: Phương trình quy về phương trình bậc hai
Bài tập cuối chương 7
Bài 1: Quy tắc cộng và quy tắc nhân
Bài 2: Hoán vị, chỉnh hợp và tổ hợp
Bài 3: Nhị thức Newton






