Giải SBT Toán 10 (Chân trời sáng tạo) Bài 3: Nhị thức Newton

Giải Sách bài tập Toán 10 Bài 3: Nhị thức Newton

Bài 1 trang 47 SBT Toán 10 Tập 2: Khai triển các biểu thức sau:

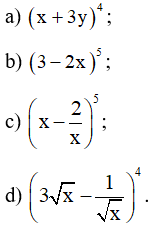
Lời giải:

a) Theo công thức nhị thức Newton ta có:

${\left(x+3y\right)}^4$= x⁴ + 4.x³.3y + 6.x².(3y)² + 4.x.(3y)³ + (3y)⁴

= x⁴ + 12x³y + 54x²y² + 108xy³ + 81y⁴.

b) Theo công thức nhị thức Newton ta có:

${\left(3-2x\right)}^5$= 3⁵ + 5.3⁴.(–2x) + 10.3³.(–2x)² + 10.3². (–2x)³ + 5.3. (–2x)⁴ + (–2x)⁵

= 243 – 810x + 1080x² – 720x³ + 240x⁴ – 32x⁵.

c) Theo công thức nhị thức Newton ta có:

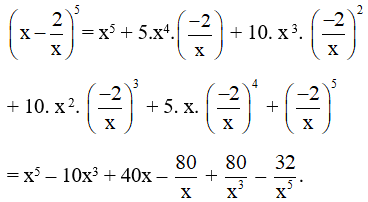
d) Theo công thức nhị thức Newton ta có:

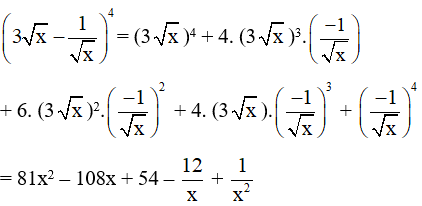
Bài 2 trang 47 SBT Toán 10 Tập 2: Khai triển và rút gọn biểu thức $\left(x-2\right){\left(2x+1\right)}^4$

Lời giải:

Ta có:

(2x + 1)⁴ = (2x)⁴ + 4.(2x)³.1 + 6.(2x)².1² + 4.2x.1³ + 1⁴

= 16x⁴ + 32x³ + 24x² + 8x + 1

Ta có

$\left(x-2\right){\left(2x+1\right)}^4$ 

= ( x – 2 ) . ( 16x⁴ + 32x³ + 24x² + 8x + 1)

= 16x⁵ + 32x⁴ + 24x³ + 8x² + x – 32x⁴ – 64x³ – 48x² – 16x – 2

= 16x⁵ – 40x³ – 40x² – 15x – 2.

Bài 3 trang 47 SBT Toán 10 Tập 2: Tìm giá trị tham số a để trong khai triển

 $\left(a+x\right){\left(1+x\right)}^4$ có một số hạng là 22x².

Lời giải:

( 1 + x )⁴ = x⁴ + 4x³ + 6x² + 4x + 1

Ta có

$\left(a+x\right){\left(1+x\right)}^4$ = ax⁴ + 4ax³ + 6ax² + 4ax + a + x⁵ + 4x⁴ + 6x³ + 4x² + x

= x⁵ + (a + 4)x⁴ + (4a + 6)x³ + (6a + 4)x² + (4a + 1)x + a

Để khai triển trên có số hạng 22x²  thì 6a + 4 = 22 hay a = 3.

Vậy a = 3 thỏa mãn yêu cầu đề bài.

Bài 4 trang 47 SBT Toán 10 Tập 2: Biết rằng trong khai triển ${\left(\text{ax}-1\right)}^5$, hệ số của x⁴ gấp bốn lần hệ số của x². Hãy tìm giá trị của tham số a.

Lời giải:

${\left(\text{ax}-1\right)}^5$ = (ax)⁵ + 5. (ax)⁴. (–1) + 10. (ax)³. (–1) ² + 10. (ax)². (–1)³ + 5.(ax).(–1)⁴ + (–1)⁵ = a⁵x⁵ – 5a⁴x⁴ + 10a³x³ – 10a²x² + 5ax – 1

Hệ số của x⁴ gấp bốn lần hệ số của x²  nên $\frac{-5{\text{a}}^4}{-10{\text{a}}^2}$ = 4 (a ≠ 0) hay a² = 8 hay a = 2$\sqrt{2}$ hoặc a = –2$\sqrt{2}$.

Vậy a = 2$\sqrt{2}$ hoặc a = –2$\sqrt{2}$.

Bài 5 trang 47 SBT Toán 10 Tập 2: Biết rằng trong khai triển của ${\left(\text{ax}+\frac{1}{x}\right)}^4$ số hạng không chứa x là 24. Hãy tìm giá trị của tham số a.

Lời giải:

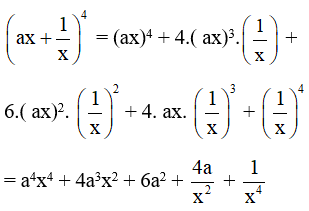
Trong khai triển, số hạng không chứa x là 24 nên 6a² = 24 hay a = 2 hoặc a = –2.

Vậy a = 2 hoặc a = – 2.

Bài 6 trang 47 SBT Toán 10 Tập 2: Cho biểu thức $A={\left(2+x\right)}^4+{\left(2-x\right)}^4$

a) Khai triển và rút gọn biểu thức A;

b) Sử dụng kết quả ở câu a, tính gần đúng $A=2,{05}^4+1,{95}^4$.

Lời giải:

a) Ta có:

(2 + x)⁴ = x⁴ + 4.x³.2 + 6.x².2² + 4.x.2³ + 2⁴

= x⁴ + 8x³ + 24x² + 32x + 16

(2 – x)⁴ = (–x)⁴ + 4.( –x)³.2 + 6. (–x)².2² + 4. (–x).2³ + 2⁴

= x⁴ – 8x³ + 24x² – 32x + 16

Suy ra

$A={\left(2+x\right)}^4+{\left(2-x\right)}^4$

= x⁴ + 8x³ + 24x² + 32x + 16 + x⁴ – 8x³ + 24x² – 32x + 16

= 2x⁴ + 48x² + 32

Vậy A = 2x⁴ + 48x² + 32.

b) $A=2,{05}^4+1,{95}^4$

A = ( 2 + 0,05 )⁴ + ( 2 – 0,05 )⁴

A = 2.0,05⁴ + 48.0,05² + 32

A ≈ 32,12

Vậy A ≈ 32,12.

Bài 7 trang 47 SBT Toán 10 Tập 2: Bạn An có 4 cái bánh khác nhau từng đôi một. An có bao nhiêu cách chọn ra một số cái bánh (tính cả trường hợp không chọn cái nào) để mang theo trong buổi dã ngoại?

Lời giải:

Trường hợp 1: An không chọn bánh nào. Có ${\text{C}}_{\text{4}}^{\text{0}}$ cách.

Trường hợp 2: An chọn 1 cái bánh. Có ${\text{C}}_{\text{4}}^{\text{1}}$ cách chọn bánh khác nhau.

Trường hợp 3: An chọn 2 cái bánh. Có ${\text{C}}_{\text{4}}^{\text{2}}$ cách chọn bánh khác nhau.

Trường hợp 4: An chọn 3 cái bánh. Có ${\text{C}}_{\text{4}}^{\text{3}}$ cách chọn bánh khác nhau.

Trường hợp 5: An chọn 4 cái bánh. Có ${\text{C}}_{\text{4}}^{\text{4}}$ cách chọn bánh khác nhau.

Áp dụng quy tắc cộng ta thấy An có:

 = ( 1 + 1 )⁴  = 2⁴ = 16 cách chọn bánh (tính cả trường hợp không chọn cái nào) để mang theo trong buổi dã ngoại.

Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác: