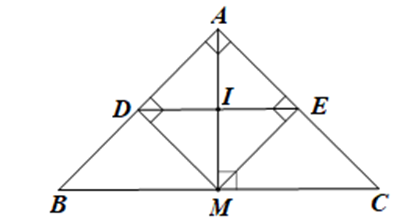
Cho tam giác ABC vuông cân tại A. Lấy điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là hình chiếu của điểm M trên đường thẳng AB, AC.
Điểm M ở vị trí nào trên cạnh BC thì DE có độ dài nhỏ nhất? Tính độ dài nhỏ nhất đó, biết AB = 2 cm.
Do ADME là hình chữ nhật nên AM = DE.
Suy ra DE có độ dài nhỏ nhất khi AM có độ dài nhỏ nhất.
Vậy M là hình chiếu của A trên đường thẳng BC.
Trong tam giác ABC vuông cân tại A, ta có:
AC = AB = 2 cm và BC2 = AB2 + AC2 = 22 + 22 = 8 (định lý Pythagore)
Suy ra \[BC = \sqrt 8 {\rm{\;cm}}\].
Xét ∆ABM vuông tại M và ∆ACM vuông tại M có:
Cạnh AM chung, \(\widehat {ABM} = \widehat {ACM}\) (do ∆ABC vuông cân tại A)
Do đó ∆ABM = ∆ACM (cạnh góc vuông – góc nhọn kề).
Suy ra \(BM = CM = \frac{{BC}}{2} = \frac{{\sqrt 8 }}{2} = \sqrt 2 {\rm{\;cm}}\).
Tam giác ABM vuông tại M có \(\widehat {ABM} = 45^\circ \) nên \(\widehat {BAM} = \widehat {ABM} = 45^\circ \).
Suy ra tam giác ABM vuông cân tại M.
Do đó \(DE = AM = BM = \sqrt 2 {\rm{\;}}\left( {{\rm{cm}}} \right)\).
Vậy \(DE = \sqrt 2 {\rm{\;cm}}\).