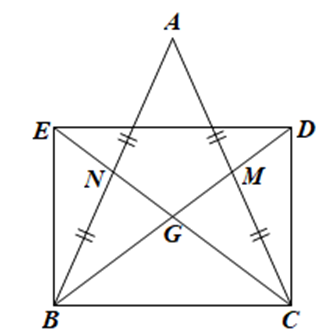
Do GD = GB, GE = GC nên G là trung điểm của BD và CE.
Tứ giác BEDC có hai đường chéo BD và CE cắt nhau tại trung điểm G của mỗi đường nên BEDC là hình bình hành.
BM, CN là các đường trung tuyến của ∆ABC nên M là trung điểm của AC, N là trung điểm của AB
Suy ra AM = CM, AN = BN
Lại có AB = AC (do ∆ABC cân tại A) nên BN = CM
Xét ∆BCM và ∆CBN có:
CM = BN (chứng minh trên), ^ABC=^ACB, cạnh BC chung
Do đó ∆BCM = ∆CBN (c.g.c). Suy ra BM = CN (hai cạnh tương ứng)
Do G là trọng tâm của tam giác ABC nên BG=23BM và CG=23CN.
Do đó BG = CG.
Mà G là trung điểm của BD và CE, suy ra BD = CE.
Hình bình hành BEDC có BD = CE nên BEDC là hình chữ nhật.