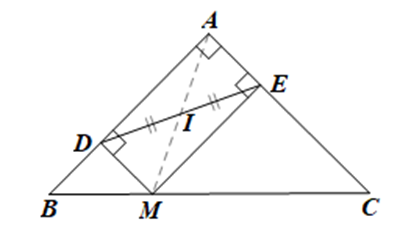
Chứng minh khi điểm M thay đổi vị trí trên cạnh BC thì chu vi của tứ giác ADME không đổi
Cho tam giác ABC vuông cân tại A. Lấy điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là hình chiếu của điểm M trên đường thẳng AB, AC.
Chứng minh khi điểm M thay đổi vị trí trên cạnh BC thì chu vi của tứ giác ADME không đổi.