Cho hình chữ nhật ABCD có hai đường chéo AC và BD Chứng minh Tứ giác AEMF là hình chữ nhật
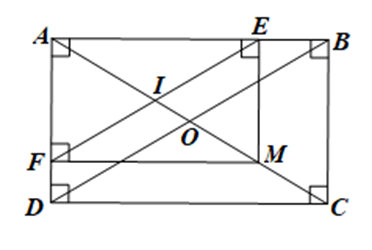
Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Lấy điểm M thuộc đoạn thẳng OC. Gọi E, F lần lượt là hình chiếu của điểm M trên đường thẳng AB, AD. Chứng minh:
Tứ giác AEMF là hình chữ nhật;