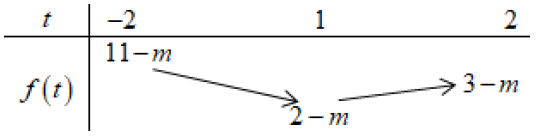Có bao nhiêu giá trị nguyên dương của m để hàm số y = căn bậc hai của ( sin x - căn bậc hai của 3 cos x)^2 - 2sin x + 2 căn bậc hai của 3cos x - m + 3 xác định với mọi x thuộc R? A. Vô s
56
24/04/2024
Có bao nhiêu giá trị nguyên dương của m để hàm số y=√(sinx−√3cosx)2−2sinx+2√3cosx−m+3 xác định với mọi x∈R?
A. Vô số.
B. 3
C. 2
D. 0
Trả lời
Đáp án C
Phương pháp:
+ Đặt t=sinx−√3cosx, tìm khoảng giá trị của t.
+ Đưa hàm số về ẩn t trên miền giá trị đã xác định được, lập BBT và kết luận.
Cách giải:
y=√(sinx−√3cosx)2−2sinx+2√3cosx−m+3
y=√(sinx−√3cosx)2−2(sinx−√3cosx)−m+3
+ Đặt t=sinx−√3cosx=2(12sinx−√32cosx)=2sin(x−π3)⇒−2≤t≤2
Khi đó hàm số trở thành y=√t2−2t−m+3∀t∈[−2;2](∗).
+ Để hàm số ban đầu xác định với mọi x∈R thì hàm số xác định với mọi t∈[−2;2].
Tức là t2−2t−m+3≥0∀t∈[−2;2].
+ Xét hàm số f(t)=t2−2t−m+3 trên [−2;2] ta có BBT:
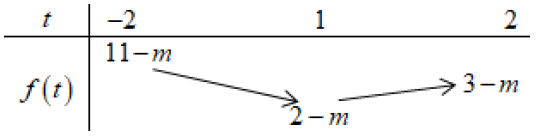
Để t2−2t−m+3≥0∀t∈[−2;2] thì 2−m≥0⇔m≤2.
Mà m nguyên dương ⇒m∈{1;2}.
Chú ý: Cần xác định chính xác khoảng giá trị của t.