Chọn B

Đặt $f\left(x\right)=x^3-3x^2-m$. Do: $SDCT\left\{\left|f\left(x\right)\right|\right\}=SDCT\left\{f\left(x\right)\right\}+SNBL\left\{f\left(x\right)\right\}$

Mà $f^{\text{'}}\left(x\right)=3x^2-6x\Rightarrow f^{\text{'}}\left(x\right)=0\iff \left[\begin{array}{l}x=0\\ x=2\end{array}\right.$ nên hàm số  f(x) có hai điểm cực trị.

Để hàm số $\left|f\left(x\right)\right|$ có nhiều điểm cực trị nhất thì phương trình f(x) = 0 có ba nghiệm phân biệt.

Khảo sát hàm số f(x) = 0 ta vẽ được được hình ảnh đồ thị hàm số như sau:

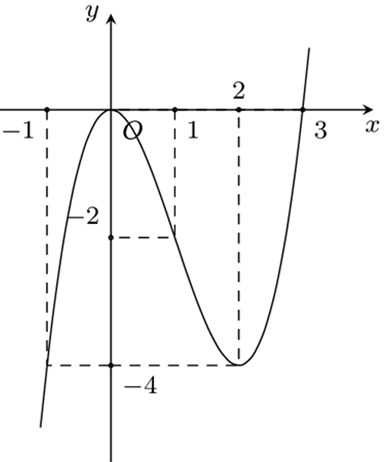
Nên phương trình $f\left(x\right)=0$ có nhiều nghiệm bội lẻ nhất khi: $-4<m<0$.

Vậy có 3 giá trị nguyên của tham số m để hàm số có nhiều điểm cực trị nhất.