Chứng minh rằng với mọi góc x ( 0° ≤ x ≤ 90°), ta đều có: a) sin x = căn ( 1 - cos ^x)
Bài 5 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng với mọi góc x ( 0° ≤ x ≤ 90°), ta đều có:
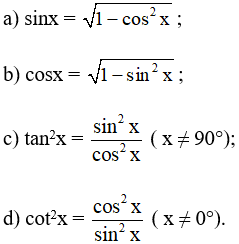
Bài 5 trang 69 SBT Toán 10 Tập 1: Chứng minh rằng với mọi góc x ( 0° ≤ x ≤ 90°), ta đều có:
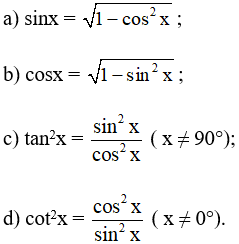
a) Ta có: cos2x + sin2x=1.
⇒ sin2x = 1 – cos2x
⇒ sinx = √1−cos2x hoặc sinx = -√1−cos2x
Vì 0° ≤ x ≤ 90° nên 0 ≤ sinx ≤ 1. Do đó chỉ có sinx = √1−cos2x là thỏa mãn.
Vậy sinx = √1−cos2x.
b) Ta có: cos2x + sin2x = 1
⇒ cos2x = 1 – sin2x.
⇒ cosx = √1−sin2x hoặc cosx = -√1−sin2x
Vì 0° ≤ x ≤ 90° nên 0 ≤ cos ≤ 1. Do đó chỉ có cosx = √1−sin2x là thỏa mãn.
Vậy cosx = √1−sin2x.
c) Ta có: tanx = sinxcosx ⇒ tan2x = sin2xcos2x( x ≠ 90°). (ĐPCM)
d) Ta có: cotx = cosxsinx ⇒ cot2x = cos2xsin2x ( x ≠ 0°). (ĐPCM)
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Giá trị lượng giác của góc từ 0° đến 180°