Cho tứ diện S. ABCD có đáy ABCD là hình thang ( AB//CD). Gọi M, N và P lần lượt là trung điểm của BC, AD, và SA. Giao tuyến của hai mặt phẳng (SAB) và (MNP). A. Đường thẳng qua M và song
30
25/04/2024
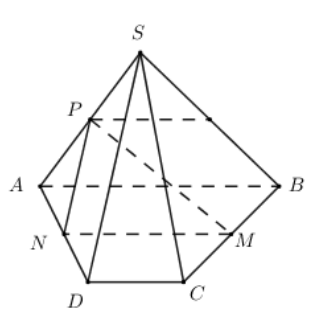
Cho tứ diện S. ABCD có đáy ABCD là hình thang \[\left( {AB//CD} \right)\]. Gọi M, N và P lần lượt là trung điểm của BC, AD, và SA. Giao tuyến của hai mặt phẳng (SAB) và (MNP).
A. Đường thẳng qua M và song song với SC.
B. Đường thẳng qua P và song song với AB.
C. Đường thẳng PM.
D. Đường thẳng qua S và song song với AB.
Trả lời
Đáp án B
Phương pháp:
Sử dụng định lí: Hai mặt phẳng chứa hai đường thẳng song song thì cắt nhau theo giao tuyến (nếu có) song song với hai đường thẳng đó.
Cách giải:
\[\left( {SAB} \right)\] và \[\left( {MNP} \right)\] có điểm P chung;
\[\left\{ \begin{array}{l}AB \subset \left( {SAB} \right)\\MN \subset \left( {MNP} \right)\\AB||MN\end{array} \right. \Rightarrow \] Giao tuyến của 2 mặt phẳng \[\left( {SAB} \right)\] và \[\left( {MNP} \right)\] là đường thẳng qua P và song song với AB.