Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên các cạnh AB, CD, BC (không trùng với các đỉnh của tứ diện ABCD sao cho PR AC. Khi đó giao tuyến của hai mặt phẳng ( PQR ) và ( ACD) song
47
23/04/2024
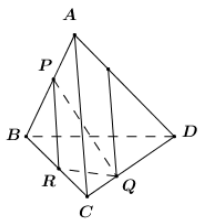
Cho tứ diện ABCD và ba điểm P, Q, R lần lượt nằm trên các cạnh AB, CD, BC (không trùng với các đỉnh của tứ diện ABCD) sao cho \[PR\parallel AC\]. Khi đó giao tuyến của hai mặt phẳng \[\left( {PQR} \right)\] và \[\left( {ACD} \right)\] song song với đường thẳng nào trong các đường thẳng sau?
A. BD
B. CD
C. CB
D. AC
Trả lời
Đáp án D
Phương pháp:
Giao tuyến của hai mặt phẳng chứa hai đường thẳng song song là đường thẳng đi qua 1 điểm chung của hai mặt phẳng và song song với hai đường thẳng đó.
Cách giải:
Ta có \[\left\{ \begin{array}{l}Q \in \left( {PQR} \right)\\Q \in CD \subset \left( {ACD} \right) \Rightarrow Q \in \left( {ACD} \right)\end{array} \right. \Rightarrow Q \in \left( {PQR} \right) \cap \left( {ACD} \right)\]
\[\left\{ \begin{array}{l}\left( {PQR} \right) \supset PR\\\left( {ACD} \right) \supset AC\\PR\parallel AC\end{array} \right. \Rightarrow \] Giao tuyến của hai mặt phẳng \[\left( {PQR} \right)\] và \[\left( {ACD} \right)\]
là đường thẳng đi qua Q và song song với AC, PR.