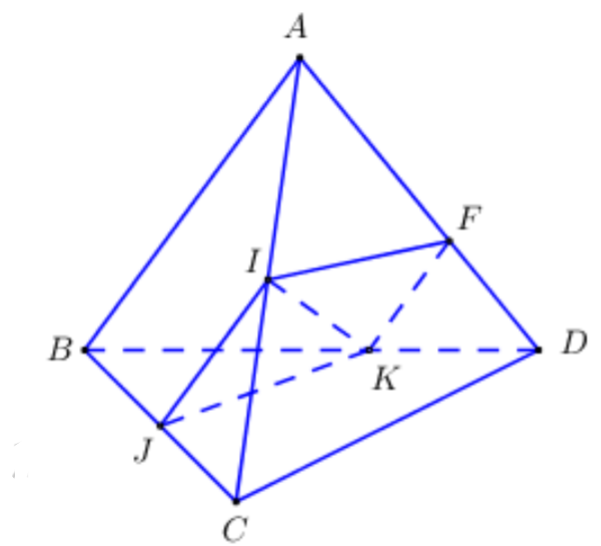
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK = 2KD. Gọi F là giao điểm của AD với mặt phẳng (IJK). Tính tỉ số FA/FD A. 7/3 B. 2
59
24/04/2024
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK = 2KD. Gọi F là giao điểm của AD với mặt phẳng (IJK). Tính tỉ số\[\frac{{FA}}{{FD}}.\]
A. \[\frac{7}{3}\]
B. 2
C. \[\frac{{11}}{5}\]
D. \[\frac{5}{3}\]
Trả lời
Đáp án B
Phương pháp:
+ Dựng giao tuyến dựa vào các yếu tố song song.
+ Sử dụng định lí Ta-lét.
Cách giải:
\[\left\{ \begin{array}{l}\left( {IJK} \right) \supset IJ\\\left( {ABD} \right) \supset AB\\IJ\parallel AB\\K \in \left( {IJK} \right) \cap \left( {ABD} \right)\end{array} \right. \Rightarrow \]Giao tuyến của hai mặt phẳng \[\left( {IJK} \right)\]và \[\left( {ABD} \right)\]là đường thẳng đi qua K và song song với IJ, AB.
Trong \[\left( {ABD} \right)\]kẻ\[KF\parallel AB\left( {F \in AD} \right)\], khi đó ta có\[\left( {IJK} \right) \cap \left( {ABD} \right) = KF \Rightarrow \left( {IJK} \right) \cap AD = F\]
Áp dụng định lí Ta-lét ta có\[\frac{{FA}}{{FD}} = \frac{{KB}}{{KD}} = 2.\]
