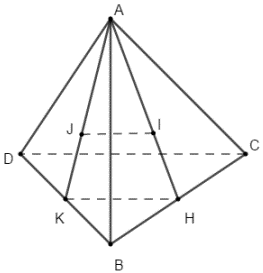
Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC, ABD. Khẳng định nào sau đây đúng? A. IJ||CD; JI = 2/3CD. B. IJ||AB; JI = 1/3CD C. IJ||AB; JI = 1/3AB. D. IJ||CD; JI = 1/3
38
23/04/2024
Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC, ABD. Khẳng định nào sau đây đúng?
A. \[IJ||CD\]; \[JI = \frac{2}{3}CD\].
B. \[IJ||AB\]; \[JI = \frac{1}{3}CD\].
C. \[IJ||AB\]; \[JI = \frac{1}{3}AB\].
D. \[IJ||CD\]; \[JI = \frac{1}{3}CD\].
Trả lời
Đáp án D
Phương pháp:
Sử dụng định lí Ta-lét đảo để chứng minh song song.
Cách giải:
Gọi H, K lần lượt là trung điểm của BC, BD \( \Rightarrow HK||CD\); \(HK = \frac{1}{2}CD\) \(\left( 1 \right)\)
\(\Delta ABC\) có trọng tâm I, trung tuyến AH\( \Rightarrow \frac{{AI}}{{AH}} = \frac{2}{3}\)
Tương tự ta có \(\frac{{AJ}}{{AK}} = \frac{2}{3}\)
\( \Rightarrow \frac{{AI}}{{AH}} = \frac{{AJ}}{{AK}} \Rightarrow JI||HK\) (Định lí ta-lét đảo); \(JI = \frac{2}{3}HK\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\); \(\left( 2 \right)\) suy ra \(JI||CD\); \(JI = \frac{1}{3}CD\)
