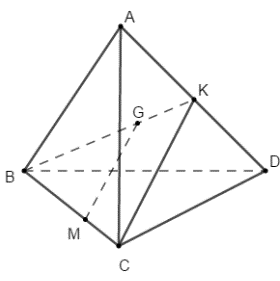
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là một điểm trên cạnh BC sao cho MB = 2MC. Khẳng định nào sau đây đúng? A. MG||( BDC). B. MG||( ABD). C. MG||( ACD). D.
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là một điểm trên cạnh BC sao cho MB=2MC. Khẳng định nào sau đây đúng?
A. MG||(BDC).
B. MG||(ABD).
C. MG||(ACD).
D. MG||(ACB).