Cho tứ diện ABCD đều cạnh a. Gọi G là trọng tâm tam giác ABC, mặt phẳng (CGD) cắt tứ diện theo một thiết diện có diện tích là: A. a^2 căn bậc hai của 2 /6 B. a^2 căn bậc hai của 3 /4
36
24/04/2024
Cho tứ diện ABCD đều cạnh a. Gọi G là trọng tâm tam giác ABC, mặt phẳng (CGD) cắt tứ diện theo một thiết diện có diện tích là:
A. \(\frac{{{a^2}\sqrt 2 }}{6}\).
B. \(\frac{{{a^2}\sqrt 3 }}{4}\).
C. \(\frac{{{a^2}\sqrt 2 }}{4}\).
D. \(\frac{{{a^2}\sqrt 3 }}{2}\).
Trả lời
Đáp án C
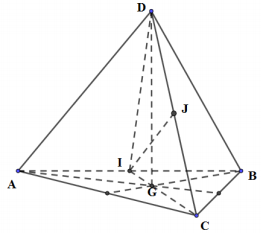
Cách giải:
Gọi I, J lần lượt là trung điểm của AB, CD \( \Rightarrow \) I, G, C thẳng hàng.
\( \Rightarrow \)(CGD) cắt tứ diện ABCD bởi thiết diện là tam giác ICD
Ta có: \(I{\rm{D}} = IC = \frac{{a\sqrt 3 }}{2}\) (do là đường cao của tam giác đều cạnh a)
\( \Rightarrow \Delta IC{\rm{D}}\) cân tại I \( \Rightarrow IJ \bot CD\)
\(\Delta IJC\) vuông tại J \( \Rightarrow IJ = \sqrt {I{C^2} - J{C^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
Diện tích \(\Delta IC{\rm{D}}\) là: \(S = \frac{1}{2}IJ.CD = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.a = \frac{{{a^2}\sqrt 2 }}{4}\).

