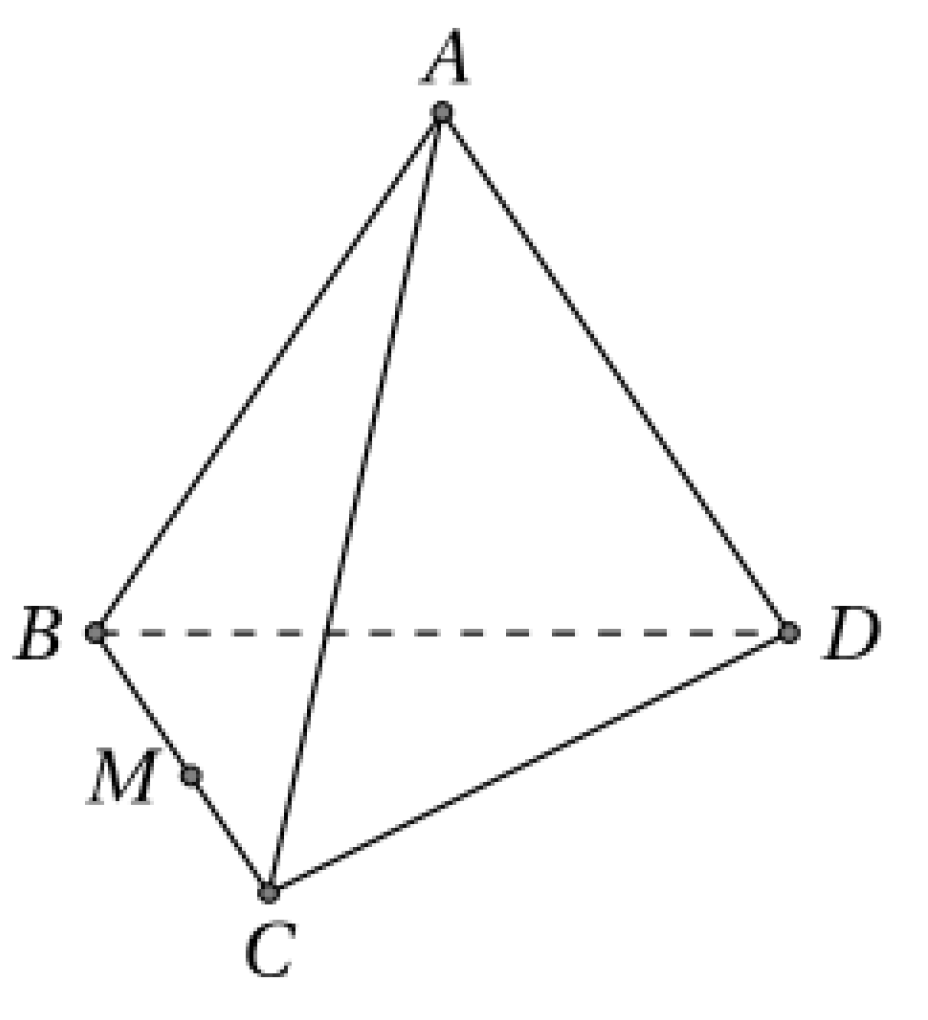
Cho tứ diện ABCD có BC = 9, AC = 6 và BD = 3 (tham khảo hình vẽ). Điểm M di chuyển trên cạnh BC. Mặt phẳng ( alpha ) qua M, song song với AC và BD cắt tứ diện theo thiết diện là một tứ giác.

Đáp án C
Phương pháp:
+ Dựng mặt phẳng \(\left( \alpha \right)\) theo mối quan hệ song song với \(AC,\,BD\)
+ Tìm thiết diện của mặt phẳng \(\left( \alpha \right)\) với hình chóp
+ Dựa vào điều kiện hình thoi và định lý Ta-lét để tính toán.
Cách giải:
Trong \(\left( {ABC} \right)\) kẻ \(MH//AC\) \(\left( {H \in AB} \right)\)
Trong \(\left( {BCD} \right)\) kẻ \(ME//DB\) \(\left( {E \in DC} \right)\)
Trong \(\left( {ABD} \right)\) kẻ \(HN//AD\) \(\left( {N \in AD} \right)\)
Suy ra \(HN//ME\).
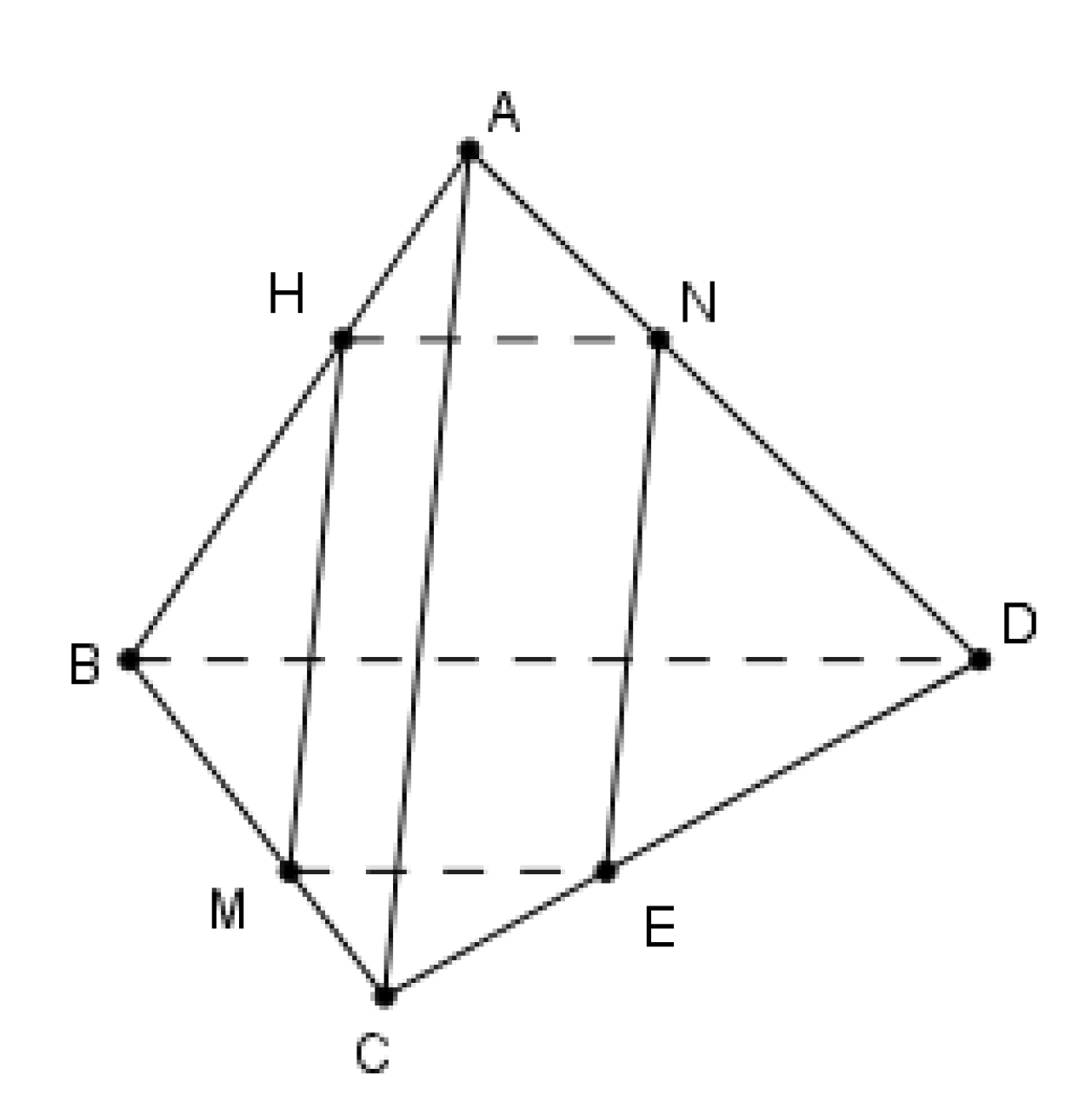
Theo định lý Ta-lét ta có: \(\frac{{HN}}{{BD}} = \frac{{AH}}{{AB}} = \frac{{MC}}{{BC}} = \frac{{ME}}{{BD}} \Rightarrow HN = ME\)
Từ đó \[MENH\] là hình bình hành.
Ta có \(\left( \alpha \right) \equiv \left( {MENH} \right)\) và \(\left\{ \begin{array}{l}\left( {MENH} \right) \cap \left( {ABC} \right) = MH\\\left( {MENH} \right) \cap \left( {BCD} \right) = ME\\\left( {MENH} \right) \cap \left( {ABD} \right) = NH\\\left( {MENH} \right) \cap \left( {ACD} \right) = NE\end{array} \right.\) nên thiết diện cần tìm là hình bình hành \[MENH\]
Để \[MENH\] là hình thoi thì \(MH = NE\)
+ Giả sử \(MC = a\,\left( {0 < a < 9} \right) \Rightarrow MB = 9 - a\)
Theo định lý Ta-lét ta có \(\frac{{ME}}{{BD}} = \frac{{MC}}{{BC}} \Leftrightarrow \frac{{ME}}{3} = \frac{a}{9} \Leftrightarrow ME = \frac{a}{3}\)
Theo định lý Ta-lét ta có \(\frac{{MH}}{{AC}} = \frac{{BM}}{{BC}} \Leftrightarrow \frac{{MH}}{6} = \frac{{9 - a}}{9} \Leftrightarrow MH = \frac{{18 - 2a}}{3}\)
Mà \(ME = MH \Leftrightarrow \frac{a}{3} = \frac{{18 - 2a}}{3} \Leftrightarrow a = 18 - 2a \Leftrightarrow a = 6\)
Suy ra \({M_0}C = 6;\,{M_0}B = 3 \Rightarrow {M_0}B.{M_0}C = 6.3 = 18\).