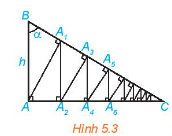
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA1 ⊥ BC, từ A1 kẻ A1A2 ⊥ AC, sau đó lại kẻ A2A3 ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA

Trả lời

Lời giải:

Tam giác AA₁B vuông tại A₁ có AB = h và \(\widehat B = \alpha \).

Do đó, AA₁ = AB sinB = h sin α.

Ta có: \(\widehat B + \widehat {BA{A_1}} = 90^\circ \) và \[\widehat {{A_1}A{A_2}} + \widehat {BA{A_1}} = 90^\circ \], suy ra \[\widehat {{A_1}A{A_2}} = \widehat B = \alpha \].

Tam giác AA₁A₂ vuông tại A₂ nên A₁A₂ = AA₁ sin\[\widehat {{A_1}A{A_2}}\] = h sin α . sin α = h sin² α.

Vì AB ⊥ AC và A₁A₂ ⊥ AC nên AB // A₁A₂, suy ra \(\widehat {{A_2}{A_1}{A_3}} = \widehat B = \alpha \) (2 góc đồng vị).

Tam giác A₁A₂A₃ vuông tại A₃ nên A₂A₃ = A­₁A₂ . sin\(\widehat {{A_2}{A_1}{A_3}}\) = h sin² α . sin α = h sin³ α.

Vì AA₁ ⊥ BC và A₂A₃ ⊥ BC nên AA₁ // A₂A₃, suy ra \(\widehat {{A_3}{A_2}{A_4}} = \widehat {{A_1}A{A_2}} = \alpha \).

Tam giác A₂A₃A₄ vuông tại A₄ nên A₃A₄ = A₂A₃ . sin\(\widehat {{A_3}{A_2}{A_4}}\) = h sin³ α . sin α = h sin⁴ α.

Cứ tiếp tục như vậy, ta xác định được A_{n – 1}A_n = h sinⁿ α.

Ta có: AA₁A₂A₃... = AA₁ + A₁A₂ + A₂A₃ + ... + A_{n – 1}A_n + ...

= h sin α + h sin² α + h sin³ α + ... + h sinⁿ α + ...

Vì góc B là góc nhọn nên sin B = sin α < 1, do đó |sin α| < 1.

Khi đó, độ dài của đường gấp khúc vô hạn AA₁A₂A₃... là tổng của cấp số nhân lùi vô hạn với số hạng đầu u₁ = h sin α và công bội q = sin α.

Do đó, AA₁A₂A₃... = \(\frac{{{u_1}}}{{1 - q}} = \frac{{h\sin \alpha }}{{1 - \sin \alpha }}\).