Bài 46 trang 93 SBT Toán 10 Tập 1: Cho tam giác nhọn ABC có các cạnh đôi một khác nhau. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp tam giác, D là điểm đối xứng với H qua O. Chứng minh rằng: .
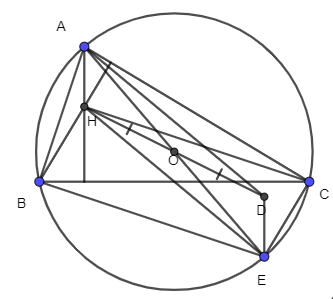
Vẽ đường kính AE
Ta có: nên AC ⊥ EC
Mà BH ⊥ EC
⇒ BH // AC (1)
Ta lại có: và AB ⊥ BE
Mà CH ⊥ AB
⇒ BE // CH (2)
Từ (1) và (2) suy ra BHEC là hình bình hành
Xét tứ giác AHDE, có:
O là trung điểm của HD (gt)
O là trung điểm của AE
Do đó AHDE là hình bình hành
Khi đó, ta có:
.
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ