Cho tam giác đều ABC cạnh a. Tính: a) |AB + BC|; b) |AB - AC| c) |AB + AC|
Bài 39 trang 92 SBT Toán 10 Tập 1: Cho tam giác đều ABC cạnh a. Tính:
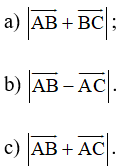
Bài 39 trang 92 SBT Toán 10 Tập 1: Cho tam giác đều ABC cạnh a. Tính:
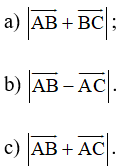
a) Ta có: →AB+→BC=→AC (quy tắc 3 điểm)
⇒ |→AB+→BC|=|→AC|=AC=a
Vậy |→AB+→BC|=a.
b) Ta có:
→AB−→AC=→AB+→CA=→CA+→AB=→CB
⇒ |→AB−→AC|=|→CB|=CB=a.
Vậy |→AB−→AC|=a.
c) Gọi D là điểm thỏa mãn ABDC là hình bình hành, M là trung điểm của BC.
Khi đó: →AB+→AC=→AD
⇒ |→AB+→AC|=|→AD|.
Xét tam giác ABC, có AM là đường trung tuyến nên AM là đường cao
⇒ AM = a√32
⇒ AD = 2AM = 2.a√32=a√3.
⇒ |→AB+→AC|=|→AD|=a√3.
Vậy |→AB+→AC|=a√3.
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ