Câu hỏi:
19/01/2024 86
Cho tam giác đều ABC cạnh bằng a, G là trọng tâm tam giác ABC. Tập hợp các điểm M thỏa mãn |→MA+→MB|=|→MA+→MC| là
Cho tam giác đều ABC cạnh bằng a, G là trọng tâm tam giác ABC. Tập hợp các điểm M thỏa mãn |→MA+→MB|=|→MA+→MC| là
A. đường trung trực đoạn thẳng BC;
A. đường trung trực đoạn thẳng BC;
B. đường tròn đường kính BC;
C. đường tròn tâm G, bán kính a;
D. đường trung trực đoạn thẳng AG.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
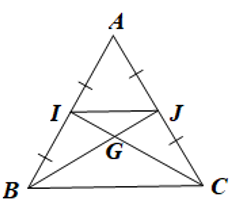
Gọi I, J lần lượt là trung điểm của AB, AC.
Khi đó {→MA+→MB=2→MI→MA+→MC=2→MJ.
Theo bài ta có |→MA+→MB|=|→MA+→MC|
⇔|2 →MI|=|2 →MJ|⇔MI=MJ.
Suy ra M nằm trên đường trung trực của đoạn thẳng IJ.
Vậy tập hợp các điểm M thỏa mãn |→MA+→MB|=|→MA+→MC| là đường trung trực của đoạn thẳng IJ.
Mà I, J lần lượt là trung điểm của AB, AC nên IJ là đường trung bình của tam giác ABC.
Do đó IJ // BC.
Suy ra tập hợp các điểm M là đường trung trực của đoạn thẳng BC.
Vậy tập hợp các điểm M là đường trung trực của đoạn thẳng BC.
Đáp án đúng là: A
Gọi I, J lần lượt là trung điểm của AB, AC.
Khi đó {→MA+→MB=2→MI→MA+→MC=2→MJ.
Theo bài ta có |→MA+→MB|=|→MA+→MC|
⇔|2 →MI|=|2 →MJ|⇔MI=MJ.
Suy ra M nằm trên đường trung trực của đoạn thẳng IJ.
Vậy tập hợp các điểm M thỏa mãn |→MA+→MB|=|→MA+→MC| là đường trung trực của đoạn thẳng IJ.
Mà I, J lần lượt là trung điểm của AB, AC nên IJ là đường trung bình của tam giác ABC.
Do đó IJ // BC.
Suy ra tập hợp các điểm M là đường trung trực của đoạn thẳng BC.
Vậy tập hợp các điểm M là đường trung trực của đoạn thẳng BC.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC, gọi M là điểm bất kì thỏa mãn |→MA+→MB+→MC|=3. Hỏi có bao nhiêu điểm M thỏa mãn đẳng thức trên?
Cho tam giác ABC, gọi M là điểm bất kì thỏa mãn |→MA+→MB+→MC|=3. Hỏi có bao nhiêu điểm M thỏa mãn đẳng thức trên?
Câu 2:
Cho ba điểm A, B, C phân biệt và không thẳng hàng, gọi M là điểm thỏa mãn →MA=x→MB+y→MC. Giá trị của x + y bằng
Cho ba điểm A, B, C phân biệt và không thẳng hàng, gọi M là điểm thỏa mãn →MA=x→MB+y→MC. Giá trị của x + y bằng
Câu 3:
Cho tam giác đều ABC cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức |2→MA+3→MB+4→MC|=|→MB−→MA| là đường tròn cố định có bán kính R. Tính bán kính R theo a.
Cho tam giác đều ABC cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức |2→MA+3→MB+4→MC|=|→MB−→MA| là đường tròn cố định có bán kính R. Tính bán kính R theo a.
Câu 4:
Cho hình chữ nhật ABCD, điểm M bất kì và số thực k dương. Biết điểm M thỏa mãn đẳng thức |→MA+→MB+→MC+→MD|=k. Quỹ tích của điểm M là
Cho hình chữ nhật ABCD, điểm M bất kì và số thực k dương. Biết điểm M thỏa mãn đẳng thức |→MA+→MB+→MC+→MD|=k. Quỹ tích của điểm M là


