Cho tam giác DEF và ABC có \[DE = \frac{1}{3}AB,\;DF = \frac{1}{3}AC,\;\widehat D = \widehat A\] (Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE. Qua M kẻ MN // BC (N ∈ AC).

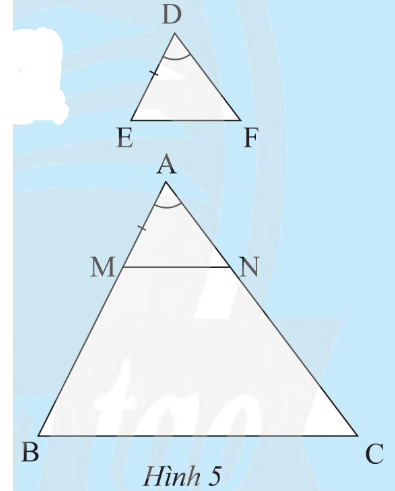
a) So sánh các tỉ số \[\frac{{AM}}{{AB}}\] và \[\frac{{AN}}{{AC}}\].

b) So sánh AN và DF.

c) Tam giác AMN có đồng dạng với tam giác ABC không?

d) Dự đoán sự đồng dạng của hai tam giác DEF và ABC.

Lời giải:

a) Tam giác ABC có MN // BC, theo định lí Thalès, ta có: \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\].

b) Ta có \[\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}};\;\frac{{DE}}{{AB}} = \frac{{DF}}{{AC}} = \frac{1}{3}\]; AM = DF suy ra AN = DF.

c) Tam giác ABC có MN cắt AB, AC lần lượt tại M và N và MN // BC.

Do đó ΔAMN ᔕ ΔABC.

d) Xét ∆DEF và ∆AMN có:

\[\widehat D = \widehat A\]

DE = AM (gt)

DF = AN (cmt)

Do đó ΔDEF = ΔAMN (c.g.c)

Dự đoán: ΔDEF ᔕ ΔABC.