Câu hỏi:
26/01/2024 87
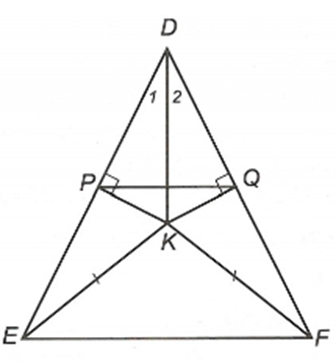
Cho ∆DEF cân tại D. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc với DF (Q ∈ DF). Khẳng định nào sau đây sai?
Cho ∆DEF cân tại D. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P ∈ DE), KQ vuông góc với DF (Q ∈ DF). Khẳng định nào sau đây sai?
A. K thuộc đường trung trực của EF;
A. K thuộc đường trung trực của EF;
B. K thuộc đường trung trực của PQ;
B. K thuộc đường trung trực của PQ;
C. DK là đường trung trực của EF;
C. DK là đường trung trực của EF;
D. DK không là đường trung trực của PQ.
D. DK không là đường trung trực của PQ.
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Ta có KE = KF (giả thiết).
Do đó K thuộc đường trung trực của EF (tính chất đường trung trực của một đoạn thẳng).
Suy ra đáp án A đúng.
Xét ∆DEK và ∆DFK, có:
DE = DF (∆DEF cân tại D).
KE = KF (giả thiết).
DK là cạnh chung.
Do đó ∆DEK = ∆DFK (cạnh – cạnh – cạnh).
Suy ra \[\widehat {{D_1}} = \widehat {{D_2}}\] (cặp góc tương ứng).
Xét ∆DPK và ∆DQK, có:
\[\widehat {DPK} = \widehat {DQK} = 90^\circ \].
DK là cạnh chung.
\[\widehat {{D_1}} = \widehat {{D_2}}\] (chứng minh trên).
Do đó ∆DPK = ∆DQK (cạnh huyền – góc nhọn).
Suy ra DP = DQ và KP = KQ (các cặp cạnh tương ứng).
Khi đó D, K thuộc đường trung trực của PQ (tính chất đường trung trực của một đoạn thẳng).
Suy ra DK là đường trung trực của PQ (tính chất đường trung trực của một đoạn thẳng).
Do đó đáp án B đúng, D sai.
Ta có KE = KF (giả thiết) và DE = DF (∆DEF cân tại D).
Suy ra DK là đường trung trực của EF (tính chất đường trung trực của một đoạn thẳng).
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Đáp án đúng là: D
Ta có KE = KF (giả thiết).
Do đó K thuộc đường trung trực của EF (tính chất đường trung trực của một đoạn thẳng).
Suy ra đáp án A đúng.
Xét ∆DEK và ∆DFK, có:
DE = DF (∆DEF cân tại D).
KE = KF (giả thiết).
DK là cạnh chung.
Do đó ∆DEK = ∆DFK (cạnh – cạnh – cạnh).
Suy ra \[\widehat {{D_1}} = \widehat {{D_2}}\] (cặp góc tương ứng).
Xét ∆DPK và ∆DQK, có:
\[\widehat {DPK} = \widehat {DQK} = 90^\circ \].
DK là cạnh chung.
\[\widehat {{D_1}} = \widehat {{D_2}}\] (chứng minh trên).
Do đó ∆DPK = ∆DQK (cạnh huyền – góc nhọn).
Suy ra DP = DQ và KP = KQ (các cặp cạnh tương ứng).
Khi đó D, K thuộc đường trung trực của PQ (tính chất đường trung trực của một đoạn thẳng).
Suy ra DK là đường trung trực của PQ (tính chất đường trung trực của một đoạn thẳng).
Do đó đáp án B đúng, D sai.
Ta có KE = KF (giả thiết) và DE = DF (∆DEF cân tại D).
Suy ra DK là đường trung trực của EF (tính chất đường trung trực của một đoạn thẳng).
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC cân tại A. Gọi M là một điểm nằm trong tam giác sao cho MB = MC, N là trung điểm của BC. Khẳng định nào sau đây đúng nhất?
Câu 2:
Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?
Cho ∆ABC có AB < AC, đường phân giác AD. Trên cạnh AC, lấy điểm E sao cho AE = AB. Kết luận nào sau đây đúng nhất?
Câu 3:
Cho ∆ABC cân tại A, đường phân giác trong của \[\widehat A\] cắt BC tại D. Khẳng định nào dưới đây sai?
Cho ∆ABC cân tại A, đường phân giác trong của \[\widehat A\] cắt BC tại D. Khẳng định nào dưới đây sai?
Câu 4:
Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
Cho ∆ABC có AB < AC. Lấy E ∈ AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC. Kẻ AH ⊥ BE tại H, AH cắt DC tại K. Chọn khẳng định đúng.
Câu 5:
Cho \[\widehat {xOy}\] (\[0^\circ < \widehat {xOy} < 90^\circ \]), Ot là tia phân giác của \[\widehat {xOy}\] và H là một điểm bất kỳ thuộc tia Ot. Qua H, lần lượt vẽ đường thẳng d và d’ thỏa mãn d vuông góc với Ox tại A, cắt Oy tại C và d’ vuông góc với Oy tại B, cắt Ox tại D. Khẳng định nào sau đây sai?
Cho \[\widehat {xOy}\] (\[0^\circ < \widehat {xOy} < 90^\circ \]), Ot là tia phân giác của \[\widehat {xOy}\] và H là một điểm bất kỳ thuộc tia Ot. Qua H, lần lượt vẽ đường thẳng d và d’ thỏa mãn d vuông góc với Ox tại A, cắt Oy tại C và d’ vuông góc với Oy tại B, cắt Ox tại D. Khẳng định nào sau đây sai?
Câu 6:
Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?
Đường thẳng d trong hình vẽ nào sau đây là đường trung trực của đoạn thẳng MN?
Câu 7:
Cho đoạn thẳng AB. Dựng các ∆PAB cân tại P, ∆QAB cân tại Q (P, Q nằm khác phía so với AB). Khẳng định nào sau đây là đúng nhất?
Cho đoạn thẳng AB. Dựng các ∆PAB cân tại P, ∆QAB cân tại Q (P, Q nằm khác phía so với AB). Khẳng định nào sau đây là đúng nhất?
Câu 8:
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\], lấy điểm I (I ≠ O). Gọi A, B lần lượt là các điểm trên các tia Ox, Oy sao cho OA = OB (O ≠ A và O ≠ B). Kết luận nào sau đây đúng nhất?
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\], lấy điểm I (I ≠ O). Gọi A, B lần lượt là các điểm trên các tia Ox, Oy sao cho OA = OB (O ≠ A và O ≠ B). Kết luận nào sau đây đúng nhất?
